题目内容
在某次数学考试中,考生的成绩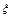 服从一个正态分布,即
服从一个正态分布,即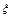 ~N(90,100).
~N(90,100).
(1)试求考试成绩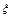 位于区间(70,110)上的概率是多少?
位于区间(70,110)上的概率是多少?
(2)若这次考试共有2 000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?
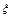 服从一个正态分布,即
服从一个正态分布,即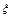 ~N(90,100).
~N(90,100).(1)试求考试成绩
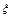 位于区间(70,110)上的概率是多少?
位于区间(70,110)上的概率是多少?(2)若这次考试共有2 000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?
(1)0.954 4(2)1 365人
∵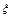 ~N(90,100),∴
~N(90,100),∴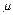 =90,
=90,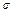 =
=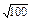 ="10. " 1分
="10. " 1分
(1)由于正态变量在区间(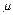 -2
-2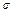 ,
,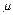 +2
+2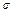 )内取值的概率是0.954 4,而该正态分布中,
)内取值的概率是0.954 4,而该正态分布中,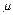 -2
-2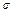 =90-2×10=70,
=90-2×10=70,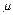 +2
+2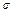 =90+2×10=110,于是考试成绩
=90+2×10=110,于是考试成绩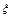 位于区间(70,110)内的概率就是0.954 4. 6分
位于区间(70,110)内的概率就是0.954 4. 6分
(2)由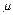 =90,
=90,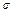 =10,得
=10,得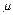 -
-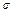 =80,
=80,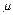 +
+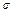 ="100. " 8分
="100. " 8分
由于正态变量在区间(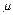 -
-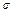 ,
,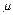 +
+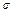 )内取值的概率是0.682 6,
)内取值的概率是0.682 6,
所以考试成绩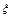 位于区间(80,100)内的概率是0.682 6. 11分
位于区间(80,100)内的概率是0.682 6. 11分
一共有2 000名考生,所以考试成绩在(80,100)间的考生大约有2 000×0.682 6≈1 365(人). 14分
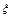 ~N(90,100),∴
~N(90,100),∴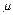 =90,
=90,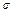 =
=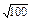 ="10. " 1分
="10. " 1分(1)由于正态变量在区间(
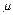 -2
-2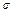 ,
,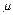 +2
+2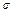 )内取值的概率是0.954 4,而该正态分布中,
)内取值的概率是0.954 4,而该正态分布中,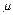 -2
-2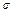 =90-2×10=70,
=90-2×10=70,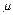 +2
+2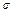 =90+2×10=110,于是考试成绩
=90+2×10=110,于是考试成绩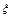 位于区间(70,110)内的概率就是0.954 4. 6分
位于区间(70,110)内的概率就是0.954 4. 6分(2)由
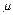 =90,
=90,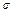 =10,得
=10,得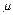 -
-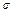 =80,
=80,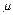 +
+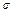 ="100. " 8分
="100. " 8分由于正态变量在区间(
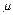 -
-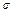 ,
,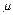 +
+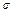 )内取值的概率是0.682 6,
)内取值的概率是0.682 6,所以考试成绩
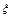 位于区间(80,100)内的概率是0.682 6. 11分
位于区间(80,100)内的概率是0.682 6. 11分一共有2 000名考生,所以考试成绩在(80,100)间的考生大约有2 000×0.682 6≈1 365(人). 14分

练习册系列答案
相关题目
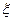 服从
服从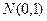 ,求下列各式的值:
,求下列各式的值: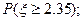 (2)
(2)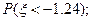 (3)
(3)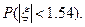
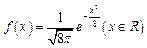 ,则总体的平均数和标准差分别是( )
,则总体的平均数和标准差分别是( ) 和
和


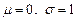 时,正态曲线为
时,正态曲线为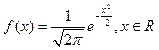 ,我们称其为标准正态曲线,且定义
,我们称其为标准正态曲线,且定义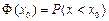 ,由此得到Φ(0)=" " .
,由此得到Φ(0)=" " .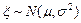 ,且
,且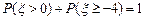 ,则
,则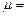 _________。
_________。  13
13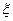 服从正态分布
服从正态分布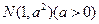 ,若
,若