Question

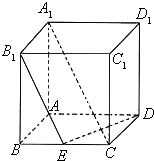（2006•宣武区一模）如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，E是BC的中点，平面B₁ED交A₁D₁于F．
（Ⅰ）指出F在A₁D₁上的位置，并证明；
（Ⅱ）求直线A₁C与B₁F所成角的余弦值；
（Ⅲ）设P为面BCC₁B₁上的动点，且AP=

2

，试指出动点P的轨迹，并求出其轨迹所表示的曲线的长度．

Answer 1

分析：（I）由正方体的性质结合面面平行的性质，证出B₁F∥DE且B₁E∥DF，得到四边形DEB₁F为平行四边形．从而有 B₁F=DE，结合A₁B₁=CD得Rt△A₁B₁F≌Rt△CDE，进而算出此时F为A₁D₁的中点；
（II）过C作CH∥DE，交AD的延长线于H，连结A₁H，则A₁C与B₁F所成的角就等于A₁C与CH所成的锐角．然后在Rt△A₁CH中，利用勾股定理和三角函数的定义加以计算，即可得出直线A₁C与B₁F所成角的余弦值；
（III）由正方体的性质和线面垂直的性质，得AB⊥BP，然后在Rt△ABP中算出BP=1，从而得到点P的轨迹是以B为圆心、半径为1的四分之一圆，利用圆的周长公式即可算出所求曲线的长度．

解答：解：（I）F为A₁D₁的中点，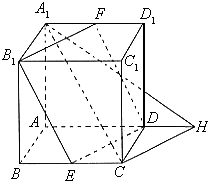
∵正方体ABCD-A₁B₁C₁D₁中，面ABCD∥面A₁B₁C₁D₁
而面B₁EDF∩面ABCD=DE，面B₁EDF∩面A₁B₁C₁D₁=B₁F
∴B₁F∥DE，
同理可得B₁E∥DF，从而得到四边形DEB₁F为平行四边形
∴B₁F=DE，
又∵A₁B₁=CD，可得Rt△A₁B₁F≌Rt△CDE
∴A1F=CE=

1

2

BC=

1

2

A1D1，得F为A₁D₁的中点…（5分）
（II）过点C作CH∥DE，交AD的延长线于H，连结A₁H，
则A₁C与B₁F所成的角就等于A₁C与CH所成的锐角．
∵Rt△A₁CH中，A1C=

3

，CH=

5

2

，A1H=

A1C2+CH2

=

13

2

∴cos∠A1CH=

A1C2+CH2-A1H2

2•A1C?CH

=

3+ 5 4 - 13 4

2• 3 • 5 2

=

15

15

即直线A₁C与B₁F所成角的余弦值为

15

15

…（10分）
（III）∵AB⊥面BCC₁B₁，BP?面BCC₁B₁，∴AB⊥BP，
在Rt△ABP中，BP=

AP2-AB2

=

( 2 )2-12

=1
由此可得点P的轨迹是以B为圆心，1为半径的四分之一圆，
可得所求曲线的长度为L=

1

4

•2π•1=

π

2

…（14分）

点评：本题在正方体中求证线面平行，并求异面直线所成角的大小，着重考查了正方体的性质、线面垂直的判定与性质和面面平行判定定理等知识，属于中档题．