题目内容
已知等比数列{an}各项均为正数,其前n项和为Sn,数列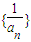 的前n项和为Tn,且S2=3T2,
的前n项和为Tn,且S2=3T2,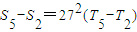 .
.(I)求数列{an}的通项公式;
(II)求数列{n•an}的前n项和Rn.
【答案】分析:(I)设公比为q,则a1>0,q>0,利用S2=3T2,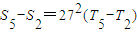 ,求出首项与公比,然后求解数列{an}的通项公式;
,求出首项与公比,然后求解数列{an}的通项公式;
(II)直利用错位相减法直接求数列{n•an}的前n项和Rn.
解答:解:(I)设公比为q,则a1>0,q>0,依题意:
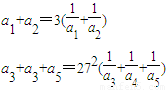
即
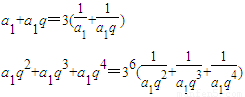 …(2分)
…(2分)
即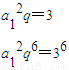 …..(3分)
…..(3分)
∵a1>0,q>0,故q=3,a1=1…..(5分)
∴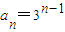 …..(6分)
…..(6分)
(II)∵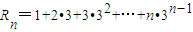 ①
①
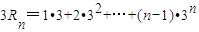 ②…(8分)
②…(8分)
①-②式有: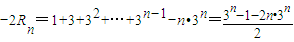
∴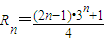 …..(12分)
…..(12分)
点评:本题考查等比数列通项公式的求法,前n循环的求法,考查错位相减法求和的应用,考查计算能力.
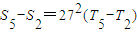 ,求出首项与公比,然后求解数列{an}的通项公式;
,求出首项与公比,然后求解数列{an}的通项公式;(II)直利用错位相减法直接求数列{n•an}的前n项和Rn.
解答:解:(I)设公比为q,则a1>0,q>0,依题意:
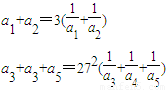
即
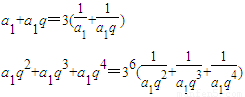 …(2分)
…(2分)即
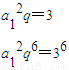 …..(3分)
…..(3分)∵a1>0,q>0,故q=3,a1=1…..(5分)
∴
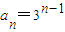 …..(6分)
…..(6分)(II)∵
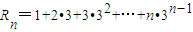 ①
①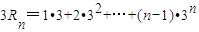 ②…(8分)
②…(8分)①-②式有:
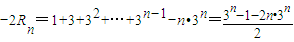
∴
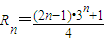 …..(12分)
…..(12分)点评:本题考查等比数列通项公式的求法,前n循环的求法,考查错位相减法求和的应用,考查计算能力.

练习册系列答案
相关题目