题目内容
已知椭圆的两个焦点分别为 ,离心率
,离心率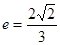 。
。
(1)求椭圆方程;
(2)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为– ,求直线l倾斜角的取值范围。
,求直线l倾斜角的取值范围。
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
【解析】
试题分析:(Ⅰ)设椭圆方程为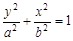
由已知,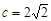 ,由
,由 解得a=3,
解得a=3,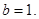
∴ 为所求
为所求
(Ⅱ)解法一:设直线l的方程为y=kx+b(k≠0)
解方程组
将①代入②并化简,得
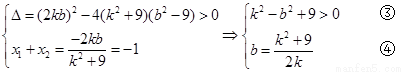
将④代入③化简后,得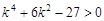 。
。
解得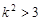 ∴
∴ , 所以倾斜角
, 所以倾斜角 。
。
解法二:(点差法)设
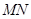 的中点为
的中点为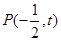 在椭圆
在椭圆 内,且直线l不与坐标轴平行。
内,且直线l不与坐标轴平行。
因此,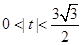 ,
,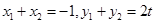
∵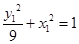 ,
,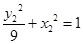
∴两式相减得 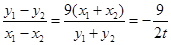
即 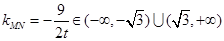
∴ 。所以倾斜角
。所以倾斜角
考点:本题主要考查椭圆的标准方程,直线与椭圆的位置关系。
点评:典型题,涉及直线与椭圆的位置关系问题,通过联立方程组得到一元二次方程,应用韦达定理可实现整体代换,简化解题过程。涉及椭圆上两点问题,可以利用“点差法”,建立连线的斜率与a,b的关系。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 :
:
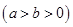 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足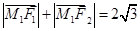 .
.
 作直线
作直线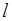 ,使得直线
,使得直线 .求出
.求出 的值.
的值. :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
. (0,
(0,  )
) ,使得过点
,使得过点 与椭圆
与椭圆 .若存在,请求出
.若存在,请求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
.
 作直线
作直线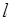 ,使得直线
,使得直线 .求出
.求出 的值.
的值.