题目内容
已知椭圆的两个焦点分别是F1(0,-2| 2 |
| 2 |
2
| ||
| 3 |
(1)求椭圆的方程;
(2)一条不与坐标轴平行的直线l与椭圆交于不同的两点M,N,且线段MN中点的横坐标为-
| 1 |
| 2 |
分析:(1)根据焦距,求得a和b的关系,利用离心率求得a和b的另一公式联立求得a和b,则椭圆的方程可得.
(2)设出直线l的方程,与椭圆的方程联立消去y,利用判别式大于0大于k和b的不等式关系,利用韦达定理表示出x1+x2和x1x2,根据MN的中点的横坐标求得k和b的关系,进而求得b的范围,分别看b≥3和b≤-3两种情况,求得k的范围,则直线的倾斜角的范围可得.
(2)设出直线l的方程,与椭圆的方程联立消去y,利用判别式大于0大于k和b的不等式关系,利用韦达定理表示出x1+x2和x1x2,根据MN的中点的横坐标求得k和b的关系,进而求得b的范围,分别看b≥3和b≤-3两种情况,求得k的范围,则直线的倾斜角的范围可得.
解答:解:(1)依题意可知
求得a=3,b=1
∴椭圆的方程为:
+ x2=1
(2)直线l不与坐标轴平行,设为y=kx+b(k≠0),M(x1,y1),N(x2,y2)
联立方程:
则(9+k2)x2+2kbx+b2-9=0
△=(2kb)2-4(9+k2)(b2-9)>0,k2-b2+9>0
x1+x2=-
,x1x2=
MN的中点的横坐标=
(x1+x2)=-
所以x1+x2=-1,可得所以9+k2=2kb,
整理得(k-b)2=b2-9≥0,故b2≥9,解得b≥3或b≤-3
又b(b-2k)<0
所以b≥3时,b-2k<0,k>
≥
b≤-3<0时,b-2k>0,k<
≤-
所以k的取值范围为(-∞,-
)∪(
,+∞)
直线l的倾斜角的取值范围为:(arctan
,
)∪(
,π-arctan
)
|
∴椭圆的方程为:
| y2 |
| 9 |
(2)直线l不与坐标轴平行,设为y=kx+b(k≠0),M(x1,y1),N(x2,y2)
联立方程:
|
△=(2kb)2-4(9+k2)(b2-9)>0,k2-b2+9>0
x1+x2=-
| 2kb |
| 9+k2 |
| b2-9 |
| 9+k2 |
MN的中点的横坐标=
| 1 |
| 2 |
| 1 |
| 2 |
所以x1+x2=-1,可得所以9+k2=2kb,
整理得(k-b)2=b2-9≥0,故b2≥9,解得b≥3或b≤-3
又b(b-2k)<0
所以b≥3时,b-2k<0,k>
| b |
| 2 |
| 3 |
| 2 |
b≤-3<0时,b-2k>0,k<
| b |
| 2 |
| 3 |
| 2 |
所以k的取值范围为(-∞,-
| 3 |
| 2 |
| 3 |
| 2 |
直线l的倾斜角的取值范围为:(arctan
| 3 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3 |
| 2 |
点评:本题主要考查了直线与圆锥曲线的关系.研究直线与圆锥曲线位置关系的问题,通常有两种方法:一是转化为研究方程组的解的问题,利用直线方程与圆锥曲线方程所组成的方程组消去一个变量后,将交点问题(包括公共点个数、与交点坐标有关的问题)转化为一元二次方程根的问题,结合根与系数的关系及判别式解决问题;二是运用数形结合,迅速判断某些直线和圆锥曲线的位置关系.

练习册系列答案
相关题目
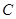 :
:
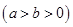 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足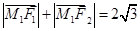 .
.
 作直线
作直线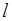 ,使得直线
,使得直线 .求出
.求出 的值.
的值. :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
. (0,
(0,  )
) ,使得过点
,使得过点 与椭圆
与椭圆 .若存在,请求出
.若存在,请求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
.
 作直线
作直线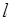 ,使得直线
,使得直线 .求出
.求出 的值.
的值.