题目内容
11.(1)已知△ABC的内角A,B,C所对的边分别为a,b,c,且a=2,cos B=$\frac{3}{5}$,b=4,求sinA的值;(2)在等比数列{an}中,a2=3,a5=81,求等比数列{an}的通项公式.
分析 (1)利用正弦定理进行求解即可求sinA的值;
(2)求出等比数列的首项和公比即可.
解答 解:(1)∵cosB=$\frac{3}{5}$,
∴sinB=$\sqrt{1-co{s}^{2}B}=\sqrt{1-(\frac{3}{5})^{2}}$=$\frac{4}{5}$,
由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$得sinA=$\frac{asinB}{b}$=$\frac{2×\frac{4}{5}}{4}$=$\frac{2}{5}$;
(2)∵a2=3,a5=81,
∴$\left\{\begin{array}{l}{{a}_{1}q=3}\\{{a}_{1}{q}^{4}=81}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{q=3}\end{array}\right.$,
则an=qn-1.
点评 本题主要考查正弦定理的应用以及等比数列的通项公式的求解,根据公式进行求解是解决本题的关键.考查学生的计算能力.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
6.数列{an}中,a1=1,${a_2}=\frac{2}{3}$,且$\frac{1}{{{a_{n-1}}}}+\frac{1}{{{a_{n+1}}}}=\frac{2}{a_n}(a∈{N^*},n≥2)$,则a6=( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{7}{2}$ | D. | 7 |
16.若θ是两条异面直线所成的角,则( )
| A. | θ∈(0,π] | B. | $θ∈(0,\frac{π}{2}]$ | C. | $θ∈[0,\frac{π}{2}]$ | D. | $θ∈(0,\frac{π}{2})$ |
3.某班的60名同学已编号1,2,3,…,60,为了解该班同学的作业情况,老师收取了号码能被5整除的12名同学的作业本,这里运用的抽样方法是( )
| A. | 简单随机抽样法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 抽签法 |
1.执行如图所示的程序框图,若输入n=6,输出的S为( )
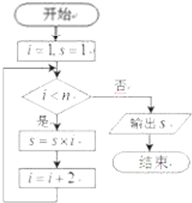

| A. | 1 | B. | 3 | C. | 7 | D. | 15 |