题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内无零点,求实数
内无零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() .(2)
.(2)![]()
【解析】
(1)求出导数![]() ,然后由
,然后由![]() 得增区间,
得增区间,![]() 得减区间.
得减区间.
(2)在![]() 上,方程
上,方程![]() 化为
化为![]() ,求出导函数
,求出导函数![]() ,
,
由![]() 时,
时,![]() ,因此对
,因此对![]() 分类讨论,
分类讨论,![]() 时,
时,![]() 恒成立,
恒成立,![]() 时,
时,![]() 有解,通过研究
有解,通过研究![]() 的单调性可得到
的单调性可得到![]() 的单调性,由零点存在定理确定有无零点.综合后可得结论.
的单调性,由零点存在定理确定有无零点.综合后可得结论.
(1)依题意,![]() .
.
令![]() ,解得
,解得![]() ,故函数
,故函数![]() 的单调增区间是
的单调增区间是![]() ,
,
由![]() ,得
,得![]() ,单调减区间是
,单调减区间是![]() .
.
(2)原方程可化为![]() ,即
,即![]() .
.
令![]() ,
,![]() ,则
,则![]() .
.
![]() 是增函数,
是增函数,![]() 时,
时,![]() ,
,
(ⅰ)当![]() 时,
时,![]() 恒成立.
恒成立.
![]() 在
在![]() 上是增函数,
上是增函数,![]() ,故原方程在
,故原方程在![]() 内无零点.
内无零点.
(ⅱ)当![]() 时,由
时,由![]() 得
得![]() ,
,![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,故
,故![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
又![]() ,
,![]() 在区间
在区间![]() 上恒小于0.∴
上恒小于0.∴![]() ,
,
下面讨论![]() 的正负;
的正负;
令![]() ,
,![]() .
.
则![]() ,
,
令![]() 是
是![]() 的导函数,
的导函数,
则![]() ,
,![]() 在
在![]() 上增函数.
上增函数.
![]() .即
.即![]() ,又
,又![]()
![]() 由零点存在性定理知,原方程在
由零点存在性定理知,原方程在![]() 上有零点.即在
上有零点.即在![]() 上有零点.
上有零点.
综上所述,所求实数![]() 的取值范围是
的取值范围是![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
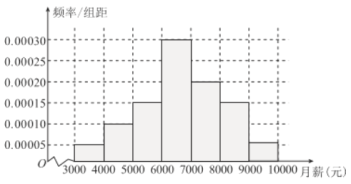
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
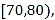
(1)从样本中日平均生产件数不足60的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(2)规定日平均生产件数不少于80的为“生产能手”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
P( | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
附: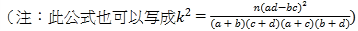
【题目】2019年,海南等8省公布了高考改革综合方案将采取“![]() ”模式,即语文、数学、英语必考,然后考生先在物理、历史中选择1门,再在思想政治、地理、化学、生物中选择2门为了更好进行生涯规划,甲同学对高一一年来的七次考试成绩进行统计分析,其中物理、历史成绩的茎叶图如图所示.
”模式,即语文、数学、英语必考,然后考生先在物理、历史中选择1门,再在思想政治、地理、化学、生物中选择2门为了更好进行生涯规划,甲同学对高一一年来的七次考试成绩进行统计分析,其中物理、历史成绩的茎叶图如图所示.
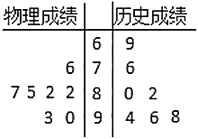
(1)若甲同学随机选择3门功课,求他选到物理、地理两门功课的概率;
(2)试根据茎叶图分析甲同学的物理和历史哪一学科成绩更稳定.(不需计算)
(3)甲同学发现,其物理考试成绩![]() (分)与班级平均分
(分)与班级平均分![]() (分)具有线性相关关系,统计数据如下表所示,试求当班级平均分为50分时,其物理考试成绩.(计算
(分)具有线性相关关系,统计数据如下表所示,试求当班级平均分为50分时,其物理考试成绩.(计算![]() ,
,![]() 时精确到0.01)
时精确到0.01)
| 57 | 61 | 65 | 72 | 74 | 77 | 84 |
| 76 | 82 | 82 | 85 | 87 | 90 | 93 |
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式: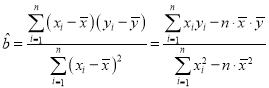 ,
,![]()