题目内容
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,常数
为自然对数的底数,常数![]() .
.
(1)求函数![]() 在区间
在区间![]() 上的零点个数;
上的零点个数;
(2)函数![]() 的导数
的导数![]() ,是否存在无数个
,是否存在无数个![]() ,使得
,使得![]() 为函数
为函数![]() 的极大值点?说明理由.
的极大值点?说明理由.
【答案】(1)1(2)存在
【解析】【试题分析】(1)对函数求导后得到函数的单调区间,利用二分法判断函数在给定区间上只有一个零点.(2)原命题等价于,存在无数个![]() ,使得
,使得![]() 成立,求得
成立,求得![]() 的表达式,构造为函数
的表达式,构造为函数![]() ,利用导数证得
,利用导数证得![]() 存在负值即可.
存在负值即可.
【试题解析】
(1)![]() ,当
,当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增;
单调递增;
因为![]() ,所以存在
,所以存在![]() ,使
,使![]() ,
,
且当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
故函数![]() 在区间
在区间![]() 上有1个零点,即
上有1个零点,即![]() .
.
(2)(法一)当![]() 时,
时, ![]() .
.
因为当![]() 时,
时, ![]() ;当
;当![]() ,
, ![]() .
.
由(1)知,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
下证:当![]() 时,
时, ![]() ,即证
,即证![]() .
.
![]() ,
,
记![]() …
…
![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
由![]() ,
,
所以存在唯一零点![]() ,使得
,使得![]() ,且
,且![]() 时,
时, ![]() 单调递减,
单调递减,
![]() 时,
时, ![]() 单调递增.
单调递增.
所以当![]() 时,
时, ![]() .……
.……
由![]() ,得当
,得当![]() 时,
时, ![]() .
.
故![]() .
.
当![]() 时,
时, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() 单调递减.
单调递减.
所以存在![]() ,使得
,使得![]() 为
为![]() 的极大值点.
的极大值点.
(2)(法二)因为当![]() 时,
时, ![]() ;当
;当![]() ,
, ![]() .
.
由(1)知,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以存在无数个![]() ,使得
,使得![]() 为函数
为函数![]() 的极大值点,即存在无数个
的极大值点,即存在无数个![]() ,使得
,使得![]() 成立, ①…由(1),问题①等价于,存在无数个
成立, ①…由(1),问题①等价于,存在无数个![]() ,使得
,使得![]() 成立,
成立,
因为![]() ,
,
记![]() …
…
![]() 因为
因为![]() ,当
,当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 单调递增,因为
单调递增,因为![]() ,
,
所以存在唯一零点![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增;
单调递增;
所以,当![]() 时,
时, ![]() , ②…
, ②…
由![]() ,可得
,可得![]() ,代入②式可得
,代入②式可得![]() ,
,
当![]() 时,
时, ![]() ,
,
所以,必存在![]() ,使得
,使得![]() ,即对任意
,即对任意![]() 有解,
有解,
所以对任意![]() ,函数
,函数![]() 存在极大值点为
存在极大值点为![]() .…
.…

 初中学业考试导与练系列答案
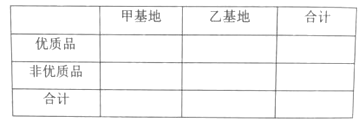
初中学业考试导与练系列答案【题目】2017年6月深圳地铁总公司对深圳地铁1号线30个站的工作人员的服务态度进行了满意度调查,其中世界之窗、白石洲、高新园、深大、桃园、大新6个站的得分情况如下:
地铁站 | 世界之窗 | 白石州 | 高新园 | 深大 | 桃园 | 大新 |
满意度得分 | 70 | 76 | 72 | 70 | 72 | x |
已知6个站的平均得分为75分.
(1)求大新站的满意度得分x,及这6个站满意度得分的标准差;
(2)从表中前5个站中,随机地选2个站,求恰有1个站得分在区间(68,75)中的概率.