题目内容
函数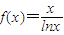
，当0＜x＜1时，下列式子大小关系正确的是（ ）A．f2（x）＜f（x2）＜f（x）
B．f（x2）＜f2（x）＜f（x）
C．f（x）＜f（x2）＜f2（x）
D．f（x2）＜f（x）＜f2（x）
【答案】分析：由0＜x＜1得到x2＜x，要比较f（x）与f（x2）的大小，即要判断函数是增函数还是减函数，可求出f′（x）利用导函数的正负决定函数的增减性．即可比较出f（x）与f（x2）大小．
解答：解：根据0＜x＜1得到x2＜x，而f′（x）=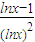
，
因为（lnx）2＞0，所以根据对数函数的单调性得到在0＜x＜1时，lnx-1＜0，所以f′（x）＜0，函数单调递减．
所以f（x2）＞f（x），根据排除法A、B、D错，C正确．
故选C
点评：考查学生利用导数研究函数的单调性，以及会利用函数的单调性判断函数值的大小，在做选择题时，可采用排除法得到正确答案．
解答：解：根据0＜x＜1得到x2＜x，而f′（x）=
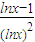，因为（lnx）2＞0，所以根据对数函数的单调性得到在0＜x＜1时，lnx-1＜0，所以f′（x）＜0，函数单调递减．
所以f（x2）＞f（x），根据排除法A、B、D错，C正确．
故选C
点评：考查学生利用导数研究函数的单调性，以及会利用函数的单调性判断函数值的大小，在做选择题时，可采用排除法得到正确答案．
练习册系列答案
相关题目
已知f（x）是周期为2的奇函数，当0＜x＜1时，f（x）=lgx．设a=f(
)，b=f(
)，c=f(
)，则（ ）
| 6 |
| 5 |
| 3 |
| 2 |
| 5 |
| 2 |
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜b＜a |
| D、c＜a＜b |