题目内容
7.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{a{\;}_{1}x+a{\;}_{2}y-3≥0}\\{x≤3}\end{array}\right.$,其中(a1,a2是等比数列{an}的前两项,且a1a2>0),若z=3x-2y的最大值为9,最小值为-2,则等比数列{an}的前n项和Sn为$\frac{1}{2}$(3n-1).分析 作出不等式组对应的平面区域,根据z=3x-2y的最大值为9,最小值为-2,求出a1=1,a2=3,结合等比数列的前n项和公式进行求解即可.
解答 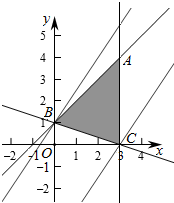 解:作出不等式组对应的平面区域,
解:作出不等式组对应的平面区域,
∵z=3x-2y的最大值为9,最小值为-2,
∴作出直线3x-2y=9和3x-2y=-2,
则由图象知3x-2y=9与x=3相交于C(3,0),
3x-2y=-2与x-y+1=0相交于B,
由$\left\{\begin{array}{l}{3x-2y=-2}\\{x-y+1=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$,即B(0,1),
则B,C在直线a1x+a2y-3=0上
则$\left\{\begin{array}{l}{3{a}_{1}-3=0}\\{{a}_{2}-3=0}\end{array}\right.$,解得a1=1,a2=3,
则公比q=3,
则等比数列{an}的前n项和Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$=$\frac{1-{3}^{n}}{1-3}$=$\frac{1}{2}$(3n-1),
故答案为:$\frac{1}{2}$(3n-1)
点评 本题主要考查线性规划以及等比数列前n项和公式的应用,根据目标函数的最值求出首项和公比是解决本题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
19.已知集合A={x|x≤-1或x≥1},B={x|a<x<a+1},且B⊆A,则实数a的取值范围是( )
| A. | a≤-2 | B. | a≥1 | C. | -2≤a≤1 | D. | a≤-2或a≥1 |
2.已知集合A={1,2,3,4,5,6},则A的子集中,含有1和3,子集有( )个.
| A. | 8 | B. | 12 | C. | 13 | D. | 16 |