Question

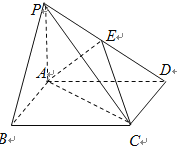
【题目】如图，在底面是矩形的四棱锥PABCD中，PA⊥平面ABCD，PA = AB = 2，BC = 4， E是PD的中点，

（1）求证： 平面EAC；

（2）求证：平面PDC⊥平面PAD；

（3）求多面体的体积．

Answer 1

【答案】（1）见解析（2）见解析（3）4

【解析】试题分析：

(1)做出辅助线，由结合线面平行的判断定理即可证得平面EAC；

(2)由题意可证得CD⊥平面PAD，结合面面垂直的判断定理即可证得平面PDC⊥平面PAD；

(3)将原问题转化为组合体体积之差的问题，分别求解体积值可得多面体的体积是4.

试题解析：

（1）连接BD交AC于点G,连接EG，因为E为PD的中点，G为BD的中点，

所以,又因为, ，

所以.

（2），，.

　　　 , . 而, 平面

. .

（3）,因为E为PD的中点， ,

所以点E到平面ADC的距离是,即 ,

所以