题目内容
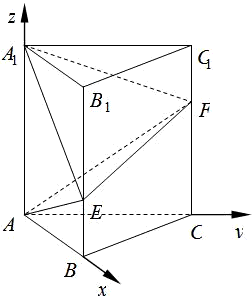
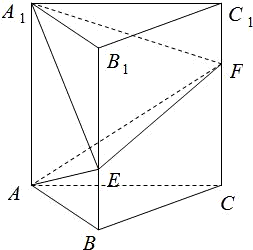 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=b,点E,F分别在棱BB1,CC1上,且
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=b,点E,F分别在棱BB1,CC1上,且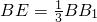 ,
,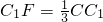 .设
.设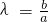 .若平面AEF⊥平面A1EF时,求λ的值.
.若平面AEF⊥平面A1EF时,求λ的值.
 解:
解:建立如图所示的空间直角坐标系A-xyz.
∵
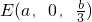 ,
, ,
,∴
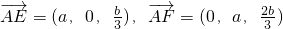 .
.设平面AEF的法向量为n1(x,y,z),
则
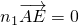 ,且
,且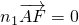 .
.即
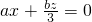 ,且
,且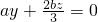 .令z=1,则
.令z=1,则 .
.∴
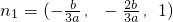 =
=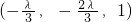 是平面AEF的一个法向量.
是平面AEF的一个法向量.同理,
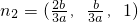 =
=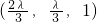 是平面A1EF的一个法向量.
是平面A1EF的一个法向量.∵平面AEF⊥平面A1EF,∴n1•n2=0.
∴
 .解得,
.解得, .
.∴当平面AEF⊥平面A1EF时,
 .(10分)
.(10分)分析:这是一直三棱柱ABC-A1B1C1中,∠BAC=90°,所以可以借助于建空间直角坐标系,利用面面垂直,可得法向量垂直来解题.进而可求λ的值.
点评:本题以一个简单的直三棱柱为载体,考查空间面面垂直的性质应用,试题的难度适中,能有效检测学生对基础知识的掌握程度和分析问题,解决问题的能力.

练习册系列答案
相关题目




