题目内容
8.已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C相交于A、B两点,则|OA|2+|OB|2(O为坐标原点)的最小值为( )| A. | 4 | B. | 8 | C. | 10 | D. | 12 |
分析 先讨论直线l的斜率不存在的情况,当直线l的斜率存在时,设直线l的方程为:y=k(x-1),与抛物线的方程联立,利用根与系数的关系表示出x1+x2,x1x2,然后把|OA|2+|OB|2表示为关于k的函数,利用函数求最小值.
解答 解:当直线l的斜率不存在,即直线l垂直于x轴时,方程为:x=1,
则A(1,2),B(1,-2).
|OA|2+|OB|2=5+5=10.
当直线l的斜率存在时,设直线l的方程为:y=k(x-1),设A(x1,y1),B(x2,y2)
由$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$得:k2x2-(2k2+4)x+k2=0,
∴${x}_{1}+{x}_{2}=\frac{2{k}^{2}+4}{{k}^{2}}$,x1x2=1,
|OA|2+|OB|2=${{x}_{1}}^{2}+{{y}_{1}}^{2}+{{x}_{2}}^{2}+{{y}_{2}}^{2}$=${{x}_{1}}^{2}+4{x}_{1}+{{x}_{2}}^{2}+4{x}_{2}$
${{(x}_{1}+{x}_{2})}^{2}-2{x}_{1}{x}_{2}+4{(x}_{1}+{x}_{2})$=$(\frac{2{k}^{2}+4}{{k}^{2}})^{2}-2+4(\frac{2{k}^{2}+4}{{k}^{2}})$
设${\frac{2{k}^{2}+4}{{k}^{2}}=t}^{\;}$,则t>2
|OA|2+|OB|2=t2+4t-2=(t+2)2-6 (t>2)
所以|OA|2+|OB|2>10.
综上可知:|OA|2+|OB|2的最小值为10.
故选:C.
点评 本题主要考查了抛物线的应用,平面解析式的基础知识.在解题过程中思维的严谨性,要考虑直线的斜率不存在的情况.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案| A. | 3 | B. | $\frac{1}{3}$ | C. | -3 | D. | $-\frac{1}{3}$ |
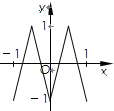
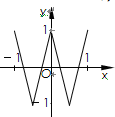
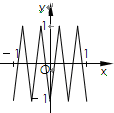
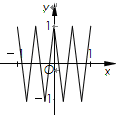
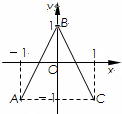 如图,函数y=f(x)的图象为折线ABC,设g(x)=f[f(x)],则函数y=g(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设g(x)=f[f(x)],则函数y=g(x)的图象为( )