题目内容
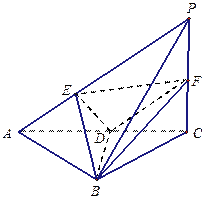
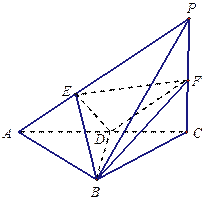
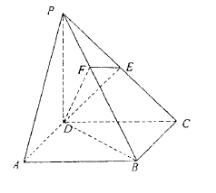
(本题满分10分) 已知三棱锥P—ABC中,PC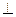 底面ABC,AB=BC,D、F分别为
底面ABC,AB=BC,D、F分别为
AC、PC的中点,DE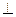 AP于E。
AP于E。
(1)求证:AP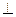 平面BDE;
平面BDE;
(2)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
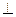 底面ABC,AB=BC,D、F分别为
底面ABC,AB=BC,D、F分别为AC、PC的中点,DE
 AP于E。
AP于E。(1)求证:AP
 平面BDE;
平面BDE;(2)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
 |
1:2
解:(1)证明: 平面ABC,
平面ABC,
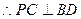 …………2分
…………2分
 由AB=BC,D为AC的中点,得
由AB=BC,D为AC的中点,得
又 ………………4分
………………4分
又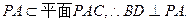
由已知
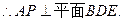 ………………………5分
………………………5分
(2)设点E和点A到平面PBC的距离分别为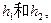
则 ………………7分
………………7分
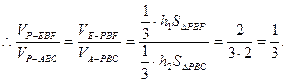
故截面BEF分三棱锥P—ABC所成上、下两部分体积的比为1:2。…………10分
 平面ABC,
平面ABC,
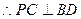 …………2分
…………2分 由AB=BC,D为AC的中点,得
由AB=BC,D为AC的中点,得
又
 ………………4分
………………4分又
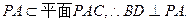
由已知

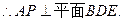 ………………………5分
………………………5分(2)设点E和点A到平面PBC的距离分别为
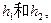
则
 ………………7分
………………7分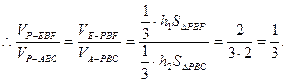
故截面BEF分三棱锥P—ABC所成上、下两部分体积的比为1:2。…………10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的交线, 已知二面角
的交线, 已知二面角 为直二面角,
为直二面角, 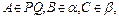
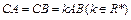 , ∠BAP=45°.
, ∠BAP=45°. 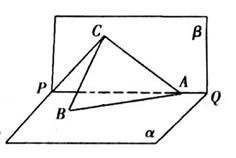
 内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?
内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?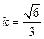 时, 求二面角B-AC-P的大小.
时, 求二面角B-AC-P的大小.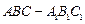 中,
中,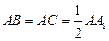 ,
,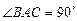 ,
,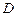 为棱
为棱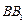 的中点.
的中点. (1)求证:
(1)求证: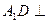 平面
平面 ;
;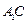 与平面ADC所成角的正弦值.
与平面ADC所成角的正弦值.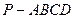 中,底面
中,底面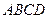 是正方形,侧棱
是正方形,侧棱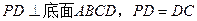 ,
, 为
为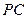 中点,作
中点,作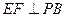 交
交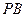 于
于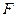
 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。 中,
中,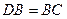 ,
, 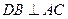 ,点
,点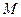 是棱
是棱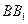 上一点.
上一点.
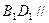 面
面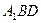 ;
;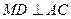 ;
;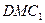
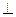 平面
平面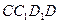 .
.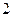 的正方体
的正方体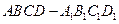 中,
中,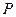 为棱
为棱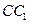 的中点,
的中点,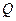 为正方形
为正方形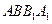 的中心,点
的中心,点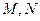 分别在直线
分别在直线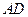 和
和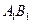 上.
上.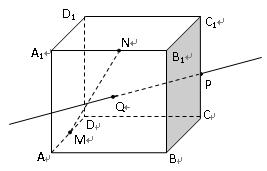
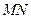 与
与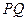 所成角的余弦值;
所成角的余弦值;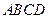 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.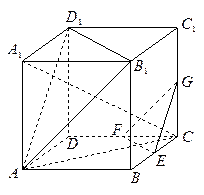
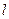 、
、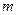 、
、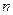 是互不相同的空间直线,
是互不相同的空间直线,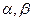 是不重合的平面,则下列命题中为真命题的是( )
是不重合的平面,则下列命题中为真命题的是( )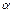 ∥β,
∥β,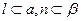 ,则
,则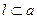 ,则
,则