题目内容
对于任意正整数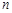 ,定义“
,定义“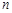
 ”如下:当
”如下:当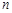 是偶数时,
是偶数时, ,
,
当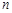 是奇数时,
是奇数时,
 .现在有如下四个命题:
.现在有如下四个命题:
① 的个位数是0;
的个位数是0;
② 的个位数是5;
的个位数是5;
③ ;
;
④ ;
;
其中正确的命题有________________(填序号)
①②③④
解析试题分析:解:①2002!!=2002×2000×…×4×2有因式10,故2002!!个位数为0,①正确;
②2003!!=2003×2001×…×3×1,其个位数字与1×3×5×7×9的个位数字相同,故为5,②正确.
③中(2003!!)(2002!!)=2003×2002×…×4×2×2009×2007×…×3×1,正确;
④2002!!=2002×2000×…×4×2=(2×1001)×(2×1000)×…×(2×2)×(2×1)=21001×1001×1000×…×2×1,故④正确,
正确的有4个.故填写①②③④
考点:本试题主要考查了新定义型问题的求解思路与方法,考查新定义型问题的理解与转化方法,体现了数学中的转化与化归的思想方法.注意与学过知识间的联系。
点评:解决该试题的关键是利用双阶乘的定义判断各个命题,要理解好双阶乘的定义,把握好双阶乘是哪些数的连乘积.

练习册系列答案
相关题目
 x2的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=______.
x2的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=______.
 的定义域为 .
的定义域为 . 都是定义在
都是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 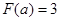 ,则
,则 ________.
________. 的定义域为
的定义域为 ,则
,则 的取值范围是 .
的取值范围是 . 的定义域是
的定义域是  ,它的值域为
,它的值域为 ,则该函数的定义域为 .
,则该函数的定义域为 . ,若
,若 使得
使得 成立,则称
成立,则称 为
为 ,有且仅有两个不动点-1,1,且
,有且仅有两个不动点-1,1,且 ,则函数
,则函数 上的函数
上的函数 满足
满足 ,则
,则
