题目内容
椭圆 的离心率为
的离心率为 ,右焦点到直线
,右焦点到直线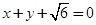 的距离为
的距离为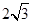 ,过
,过 的直线
的直线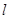 交椭圆于
交椭圆于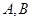 两点
两点 .
.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 若直线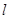 交
交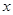 轴于
轴于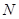 ,
,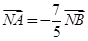 ,求直线
,求直线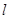 的方程
的方程 .
.
 的离心率为
的离心率为 ,右焦点到直线
,右焦点到直线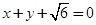 的距离为
的距离为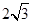 ,过
,过 的直线
的直线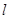 交椭圆于
交椭圆于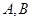 两点
两点 .
.(Ⅰ) 求椭圆的方程;
(Ⅱ) 若直线
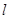 交
交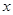 轴于
轴于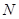 ,
,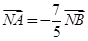 ,求直线
,求直线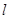 的方程
的方程 .
.(Ⅰ)设右焦点为 ,则
,则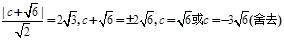 ……2分
……2分
又离心率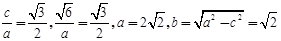 ,
,
故椭圆方程为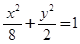 。……………………………5分
。……………………………5分
(Ⅱ)设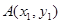 ,
, ,
,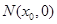 ,因为
,因为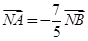 ,所以
,所以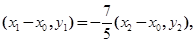
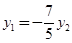 …① …………………………………7分
…① …………………………………7分
易知当直线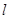 的斜率不存在或斜率为0时①不成立,于是设
的斜率不存在或斜率为0时①不成立,于是设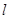 的方程为
的方程为 ,
,
联立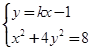 消
消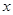 得
得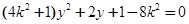 …② ……………………9分
…② ……………………9分
于是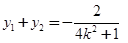 …③
…③ 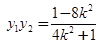 …④ …………………………11分
…④ …………………………11分
由①③得, 代入④整理得
代入④整理得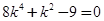 ,于是
,于是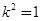 ,此时②的断别式
,此时②的断别式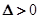 ,于是直线
,于是直线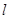 的方程是
的方程是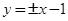 .
.
 ,则
,则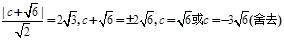 ……2分
……2分又离心率
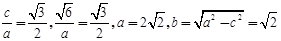 ,
,故椭圆方程为
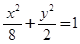 。……………………………5分
。……………………………5分(Ⅱ)设
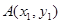 ,
, ,
,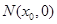 ,因为
,因为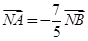 ,所以
,所以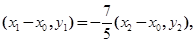
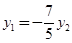 …① …………………………………7分
…① …………………………………7分易知当直线
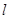 的斜率不存在或斜率为0时①不成立,于是设
的斜率不存在或斜率为0时①不成立,于是设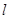 的方程为
的方程为 ,
,联立
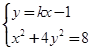 消
消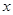 得
得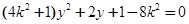 …② ……………………9分
…② ……………………9分于是
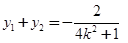 …③
…③ 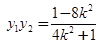 …④ …………………………11分
…④ …………………………11分由①③得,
 代入④整理得
代入④整理得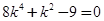 ,于是
,于是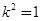 ,此时②的断别式
,此时②的断别式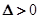 ,于是直线
,于是直线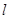 的方程是
的方程是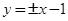 .
.略

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
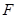 是椭圆
是椭圆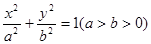 的左焦点,
的左焦点,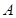 是椭圆短轴上的一个顶点,椭圆的离心率为
是椭圆短轴上的一个顶点,椭圆的离心率为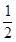 ,点
,点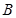 在
在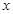 轴上,
轴上,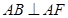 ,
,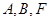 三点确定的圆
三点确定的圆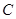 恰好与直线
恰好与直线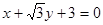 相切.
相切.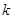
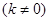 的直线
的直线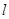 交椭圆于
交椭圆于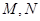 两点,
两点,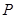 为线段
为线段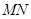 的中点,设
的中点,设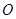 为椭圆中心,射线
为椭圆中心,射线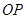 交椭圆于点
交椭圆于点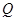 ,若
,若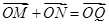 ,若存在求
,若存在求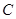 :
: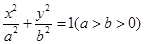 的右焦点为
的右焦点为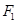
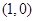 ,离心率为
,离心率为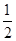 .
.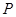 的坐标;
的坐标;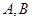 两点,若
两点,若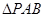 的面积为
的面积为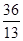 ,求直线
,求直线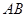 的方程.
的方程.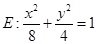 焦点为
焦点为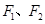 ,双曲线
,双曲线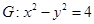 ,设
,设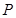 是双曲线
是双曲线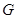 上
上 异于顶点的任一点,直线
异于顶点的任一点,直线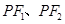 与椭圆的交点分别为
与椭圆的交点分别为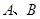 和
和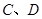 。
。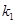 和
和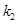 ,求
,求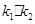 的值;
的值;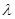 ,使得
,使得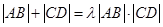 恒成立?若存在,试求出
恒成立?若存在,试求出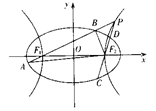
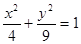 .
.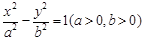 ,两焦点为
,两焦点为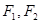 ,过
,过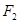 作
作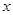 轴的垂线交双曲线于
轴的垂线交双曲线于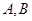 两点,且
两点,且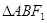 内切圆的半径为
内切圆的半径为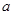 ,则此双曲线的离心率为 ▲ .
,则此双曲线的离心率为 ▲ . 的离心率是
的离心率是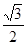 ,则双曲线
,则双曲线 =1的离心率是______。
=1的离心率是______。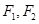 是椭圆的两焦点,
是椭圆的两焦点,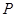 为椭圆上一点,若
为椭圆上一点,若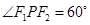 ,则离心率
,则离心率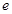 的范围是___________.
的范围是___________.