题目内容
（2013•广州二模）某单位有A、B、C三个工作点，需要建立一个公共无线网络发射点0，使得发射点到 三个工作点的距离相等．已知这三个工作点之间的距离分别为AB=80m，BC=70m，CA=50m．假定A、B、C、O四点在同一平面内．
（1）求∠BAC的大小；
（2）求点O到直线BC的距离．
（1）求∠BAC的大小；
（2）求点O到直线BC的距离．
分析：（1）△ABC中，由余弦定理求得cosA 的值，即可求得 A 的值．
（2）过点O作OD⊥BC，D为垂足，则OD即为所求．由O为△ABC的外心，可得∠BOC=120°，故∠BOD=60°，
且D为BC的中点，BD=35．在 Rt△BOD中，根据tan∠BOD=tan60°=
，求得OD的值．
（2）过点O作OD⊥BC，D为垂足，则OD即为所求．由O为△ABC的外心，可得∠BOC=120°，故∠BOD=60°，
且D为BC的中点，BD=35．在 Rt△BOD中，根据tan∠BOD=tan60°=
| BD |
| OD |
解答：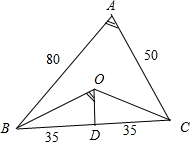
解：（1）△ABC中，由于AB=80m，BC=70m，CA=50m，由余弦定理可得
cosA=
=
=
，故有 A=60°，即∠BAC=60°．
（2）过点O作OD⊥BC，D为垂足，则O到直线BC的距离即为OD．
由于点O到、AB、C三点的距离相等，故O为△ABC的外心．
由∠BAC=60°可得∠BOC=120°，故∠BOD=60°，且D为BC的中点，BD=35．
Rt△BOD中，tan∠BOD=tan60°=
=
=
，解得 OD=
．
即O到直线BC的距离
解：（1）△ABC中，由于AB=80m，BC=70m，CA=50m，由余弦定理可得cosA=
| AB2+AC2-BC2 |
| 2AB•AC |
| 802+502-702 |
| 2×80×50 |
| 1 |
| 2 |
（2）过点O作OD⊥BC，D为垂足，则O到直线BC的距离即为OD．
由于点O到、AB、C三点的距离相等，故O为△ABC的外心．
由∠BAC=60°可得∠BOC=120°，故∠BOD=60°，且D为BC的中点，BD=35．
Rt△BOD中，tan∠BOD=tan60°=
| 3 |
| BD |
| OD |
| 35 |
| OD |
35
| ||
| 3 |
即O到直线BC的距离
35
| ||
| 3 |
点评：本题主要考查正弦定理和余弦定理的应用，直角三角形中的边角关系，属于中档题．
练习册系列答案
相关题目