题目内容
二次函数f(x)满足f(2+x)=f(2-x),又f(x)在[0,2]上是增函数,且f(a)≥f(0),则实数a的取值范围是
[ ]
A.a≥0 B.a≤0
C.0≤a≤4 D.a≤0或a≥4
答案:C
解析:
解析:
|
解析:考查二次函数的单调性。若函数
满足
又
由已知又可得
即应选C。 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,求该一元二次函数的解析式。
,求该一元二次函数的解析式。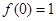 ,
,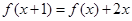
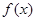
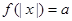
 的解的个数
的解的个数