题目内容
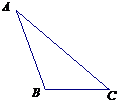
如图,在△ABC中,AC=2,BC=1,cosC=
(1)求AB的值;
(2)求sinB的值.
| 3 |
| 4 |
(1)求AB的值;
(2)求sinB的值.

(1)由AC=2,BC=1,cosC=
根据余弦定理得:AB2=AC2+BC2-2AC•BC•cosC=4+1-3=2,
解得:AB=
;
(2)∵cosC=
,且C为三角形的内角,
∴sinC=
=
,又AB=
,AC=2,
根据正弦定理
=
得:sinB=
=
.
| 3 |
| 4 |
根据余弦定理得:AB2=AC2+BC2-2AC•BC•cosC=4+1-3=2,
解得:AB=
| 2 |
(2)∵cosC=
| 3 |
| 4 |
∴sinC=
| 1-cos2C |
| ||
| 4 |
| 2 |
根据正弦定理
| AC |
| sinB |
| AB |
| sinC |
2×
| ||||
|
| ||
| 4 |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
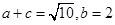 ,求△ABC的面积.
,求△ABC的面积. (1)求证:
(1)求证: ; (2)设圆O过A,B,C三点,点P位于劣弧
; (2)设圆O过A,B,C三点,点P位于劣弧 上,∠PAB=60°,求四边形ABCP的面积。
上,∠PAB=60°,求四边形ABCP的面积。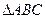 中,A、B、C为它的三个内角,设向量
中,A、B、C为它的三个内角,设向量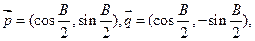 且
且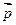 与
与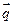 的夹角为
的夹角为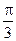 .(Ⅰ)求角
.(Ⅰ)求角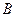 的大小; (Ⅱ) 已知
的大小; (Ⅱ) 已知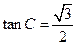 ,求
,求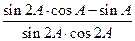 的值.
的值.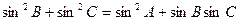 ,且
,且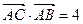 ,求△ABC的面积
,求△ABC的面积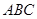 中,角
中,角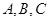 的对边分别为
的对边分别为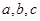 ,若
,若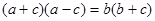 ,则
,则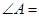 ( )
( )