题目内容
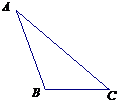
(本题满分12分)在△ABC中,三个内角是A,B,C的对边分别是a,b,c,其中c=10,且 (1)求证:
(1)求证: ; (2)设圆O过A,B,C三点,点P位于劣弧
; (2)设圆O过A,B,C三点,点P位于劣弧 上,∠PAB=60°,求四边形ABCP的面积。
上,∠PAB=60°,求四边形ABCP的面积。
 (1)求证:
(1)求证: ; (2)设圆O过A,B,C三点,点P位于劣弧
; (2)设圆O过A,B,C三点,点P位于劣弧 上,∠PAB=60°,求四边形ABCP的面积。
上,∠PAB=60°,求四边形ABCP的面积。(2)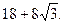
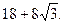
(1)证明:根据正弦定理得,
整理为: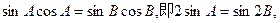
因为0<A<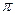 ,0<B<
,0<B<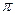 ,所以0<2A<2
,所以0<2A<2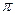 ,0<2B<2
,0<2B<2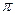 ,所以A=B,或者A+B=
,所以A=B,或者A+B=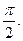 3分
3分
由于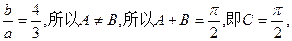 6分
6分
(2)由(1)可得:a="6,b=8. " 在Rt△ABC中,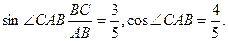
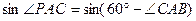
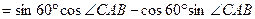
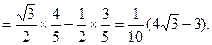 8分
8分
连结PB,在Rt△APB中,AP=AB·cos∠PAB=5。所以四边形ABCP的面积S四边形△ABCP=S△ABC+S△PAC
=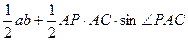
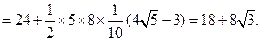

整理为:
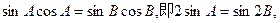
因为0<A<
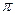 ,0<B<
,0<B<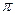 ,所以0<2A<2
,所以0<2A<2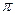 ,0<2B<2
,0<2B<2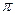 ,所以A=B,或者A+B=
,所以A=B,或者A+B=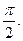 3分
3分由于
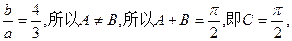 6分
6分(2)由(1)可得:a="6,b=8. " 在Rt△ABC中,
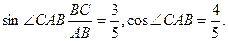
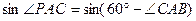
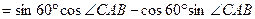
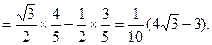 8分
8分连结PB,在Rt△APB中,AP=AB·cos∠PAB=5。所以四边形ABCP的面积S四边形△ABCP=S△ABC+S△PAC
=
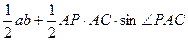
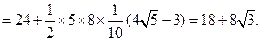

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 在数学研究性学习活动中,某小组要测量河对面
在数学研究性学习活动中,某小组要测量河对面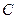 和
和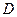 两个建筑物的距离,作图如下,所测得的数据为
两个建筑物的距离,作图如下,所测得的数据为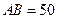 米,
米,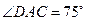 ,
,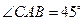 ,
,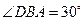 ,
,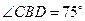 ,请你帮他们计算一下,河对岸建筑物
,请你帮他们计算一下,河对岸建筑物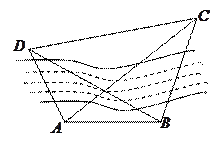
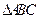 中,角
中,角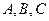 所对的边分别为
所对的边分别为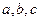 且
且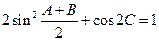 (1)求角的
(1)求角的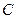 大小(2)若向量
大小(2)若向量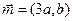 ,向量
,向量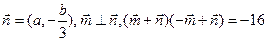 ,求
,求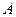 、
、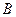 、
、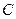 是
是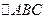 的三个内角,向量
的三个内角,向量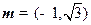 ,
,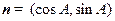 且
且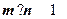 .(1)求角
.(1)求角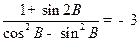 ,求
,求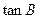 .
.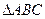 中,内角
中,内角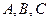 的对边分别为
的对边分别为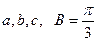 ,
,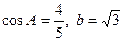 。(1)求边
。(1)求边 的大小;(2)求
的大小;(2)求
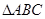 中,已知
中,已知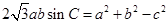 ,则
,则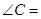 .
.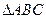 中,
中,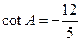 ,则
,则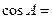


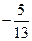
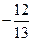
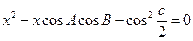 有一个根为1,则
有一个根为1,则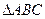 一定是( )
一定是( )