Question

【题目】已知椭圆C： =1（a＞b＞0）的离心率为 ，b= ．
（1）求椭圆C的标准方程；
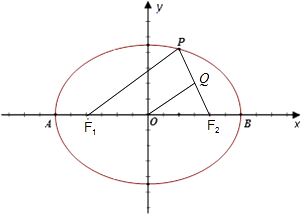
（2）F1 ， F2分别为椭圆的左、右焦点，A、B为椭圆的左、右顶点，P为椭圆C上的点，求证：以PF2为直径的圆与以AB为直径的圆相切；
（3）过左焦点F1作互相垂直的弦MN与GH，判断MN的中点与GH的中点所在直线l是否过x轴上的定点，如果是，求出定点坐标，如果不是，说出理由．

Answer 1

【答案】
（1）解：椭圆离心率e= = = ，

由b= ，解得：a2=9，

椭圆标准方程：

（2）证明：由（1）知c=2，F1（﹣2，0），F2（2，0），

连结PF1，设PF2中点Q

∵O为F1F2中点，Q为PF2中点

∴OQ∥PF1，OQ= PF1

∴OQ= PF1= （2a﹣PF2）=a﹣ PF2，

∴圆O与圆Q相切（内切）

（3）解：1°当直线MN、GH与坐标轴不垂直时，

设MN方程为x=my﹣2，m∈R，M（x1，y1），N（x2，y2），

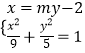∴ ，整理得（5m2+9）y2﹣20my﹣25=0

∴y1+y2= ，则x1+x2= ，

∴MN中点S（ ， ）

用﹣ 代S点坐标中的m，可得

GH中点T（ ， ）

设过x轴上的定点为（x0，0）

∴ = ，

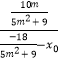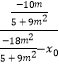化简得（14x2+18）m2+14x0+18=0，

∵m∈R，

∴14x0+18=0，即x0=﹣ ，

∴过定点（﹣ ，0）．

2°当直线MN、GH分别与坐标轴垂直时，中点分别为F1、O，

显然F1O所在直线为y=0，也过（﹣ ，0），

综上，直线l过定点（﹣ ，0）．

【解析】（1）椭圆离心率e= = = ，即b= ，即可求得a，即可求得椭圆C的标准方程；（2）由O为F1F2中点，Q为PF2中点，OQ∥PF1 ， OQ= PF1 ， 则OQ=a﹣ PF2 ， 即可证明圆O与圆Q相切；（3）分类当直线MN、GH与坐标轴不垂直时，设直线方程，代入椭圆方程，利用韦达定理及中点坐标公式即可求得MN中点S，GH中点T，直线的两点式，整理即可求得x0；当直线MN、GH分别与坐标轴垂直时，中点分别为F1、O，显然F1O所在直线为y=0，也过（﹣ ，0）．