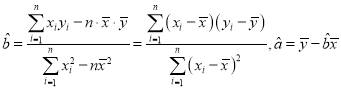[题目]在平面直角坐标系中.点是曲线:(为参数)上的动点.以坐标原点为极点.轴的正半轴为极轴建立极坐标系.以极点为中心.将线段顺时针旋转得到.设点的轨迹为曲线．(1)求曲线.的极坐标方程,(2)在极坐标系中.点的坐标为.射线与曲线分别交于两点.求的面积．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在平面直角坐标系中，点是曲线：（为参数）上的动点，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，以极点为中心，将线段顺时针旋转得到，设点的轨迹为曲线．

（1）求曲线，的极坐标方程；

（2）在极坐标系中，点的坐标为，射线与曲线分别交于两点，求的面积．

【答案】（1）；（2）.

【解析】

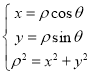（1）因为曲线：，可得的直角坐标方程为，根据极坐标与直角坐标的互化公式:，结合已知，即可求得答案.

（2）由题意知点到射线的距离为，由（1）知的极坐标方程为，即可求得答案.

（1）曲线：

的直角坐标方程为，

其极坐标方程为

设点的极坐标为，则对应的点的极坐标为

又点在上，将线段顺时针旋转得到，设点的轨迹为曲线

即的极坐标方程为

（2）由题意知点到射线的距离为，

由（1）知的极坐标方程为，

，

练习册系列答案

相关题目

【题目】如图1，在平行四边形中，，，，以对角线为折痕把折起，使点到图2所示点的位置，使得.

（Ⅰ）求证:平面平面；

(Ⅱ)求二面角的余弦值.

【题目】已知函数().

（1）若,求函数的单调区间;

（2）当时,若函数在上的最大值和最小值的和为1,求实数的值.

【题目】如图，在四棱锥中，平面，，为的中点．

（1）求证：平面；

（2）求二面角的余弦值．

【题目】在平面直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）求直线的普通方程和曲线的直角坐标方程；

（2）若直线与曲线交于、两点，求的面积.

【题目】已知函数．

（1）讨论的单调性；

（2）当时，恒成立，求的取值范围．

【题目】下图是一块平行四边形园地，经测量，.拟过线段上一点设计一条直路（点在四边形的边上，不计直路的宽度），将该园地分为面积之比为的左，右两部分分别种植不同花卉.设（单位：m）.

（1）当点与点重合时，试确定点的位置；

（2）求关于的函数关系式；

（3）试确定点的位置，使直路的长度最短.

【题目】某调查机构为了了解某产品年产量x(吨)对价格y(千克/吨)和利润z的影响，对近五年该产品的年产量和价格统计如下表：

x	1	2	3	4	5
y	17.0	16.5	15.5	13.8	12.2

（1）求y关于x的线性回归方程；

（2）若每吨该产品的成本为12千元，假设该产品可全部卖出，预测当年产量为多少时，年利润w取到最大值？

参考公式：

【题目】关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的浦丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计的值：先请全校名同学每人随机写下一个都小于的正实数对；再统计两数能与构成钝角三角形三边的数对的个数；最后再根据统计数估计的值，那么可以估计的值约为（）

A.B.C.D.

试题分类