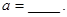题目内容
已知f(x)＝x2＋ax＋3－a，若当x∈[－2,2]时，f(x)≥0恒成立，求a的取值范围．
－7≤a≤2.
解：f(x)＝x2＋ax＋3－a＝(x＋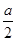
)2－
＋3－a.
①当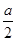－<－2，即a>4时，f(x)min＝f(－2)＝7－3a≥0，
∴a≤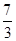
，又a>4，
故此时a不存在．
②当－2≤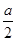－≤2，即－4≤a≤4时，f(x)min＝f(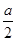－)＝3－a－≥0，
∴a2＋4a－12≤0.
∴－6≤a≤2.
又－4≤a≤4，∴－4≤a≤2.
③当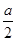－>2，即a<－4时，f(x)min＝f(2)＝7＋a≥0，
∴a≥－7.
又a<－4，故－7≤a<－4.
综上得－7≤a≤2.
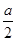)2－＋3－a.①当－
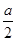<－2，即a>4时，f(x)min＝f(－2)＝7－3a≥0，∴a≤
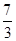，又a>4，故此时a不存在．
②当－2≤－
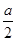≤2，即－4≤a≤4时，f(x)min＝f(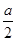－)＝3－a－≥0，∴a2＋4a－12≤0.
∴－6≤a≤2.
又－4≤a≤4，∴－4≤a≤2.
③当－
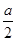>2，即a<－4时，f(x)min＝f(2)＝7＋a≥0，∴a≥－7.
又a<－4，故－7≤a<－4.
综上得－7≤a≤2.
练习册系列答案
相关题目
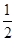四个值，则对应于曲线C1，C2，C3，C4的n值依次为( )
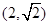，则 f（4）= ．
的图像过点
，若
，则实数
的值为（ ）
时，幂函数
为减函数，则实数
( )
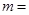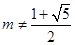
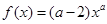，则