题目内容
如图,在四棱锥P—ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=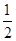 AD=1,CD=
AD=1,CD= .
.
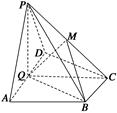
(1)若点M是棱PC的中点,求证:PA∥平面BMQ;
(2)若二面角M—BQ—C为30°,设PM=tMC,试确定t的值.
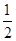 AD=1,CD=
AD=1,CD= .
.
(1)若点M是棱PC的中点,求证:PA∥平面BMQ;
(2)若二面角M—BQ—C为30°,设PM=tMC,试确定t的值.
(1)见解析 (2)t=3.
(1)证明 连接AC,交BQ于N,连接MN.
∵BC∥AD且BC=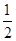 AD,
AD,
即BC綊AQ.
∴四边形BCQA为平行四边形,且N为AC中点,
又∵点M是棱PC的中点,
∴MN∥PA.
∵MN?平面BMQ,PA?平面BMQ,
∴PA∥平面BMQ.
(2)解 ∵PA=PD,Q为AD的中点,
∴PQ⊥AD.∵平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为n=(0,0,1);
Q(0,0,0),P(0,0, ),B(0,
),B(0, ,0),C(-1,
,0),C(-1, ,0).
,0).
设M(x,y,z),则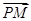 =(x,y,z-
=(x,y,z- ),
),
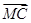 =(-1-x,
=(-1-x, -y,-z),
-y,-z),
∵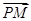 =t
=t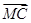 ,
,
∴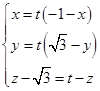 ∴
∴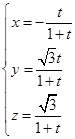
在平面MBQ中, =(0,
=(0, ,0),
,0),
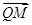 =
=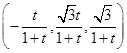 ,
,
∴平面MBQ的法向量为m=( ,0,t).
,0,t).
∵二面角M—BQ—C为30°,
cos 30°=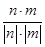 =
=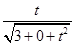 =
=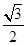 ,∴t=3.
,∴t=3.
∵BC∥AD且BC=
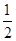 AD,
AD,即BC綊AQ.
∴四边形BCQA为平行四边形,且N为AC中点,
又∵点M是棱PC的中点,
∴MN∥PA.
∵MN?平面BMQ,PA?平面BMQ,
∴PA∥平面BMQ.
(2)解 ∵PA=PD,Q为AD的中点,
∴PQ⊥AD.∵平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.

则平面BQC的法向量为n=(0,0,1);
Q(0,0,0),P(0,0,
 ),B(0,
),B(0, ,0),C(-1,
,0),C(-1, ,0).
,0).设M(x,y,z),则
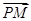 =(x,y,z-
=(x,y,z- ),
),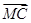 =(-1-x,
=(-1-x, -y,-z),
-y,-z),∵
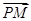 =t
=t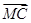 ,
,∴
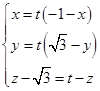 ∴
∴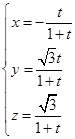
在平面MBQ中,
 =(0,
=(0, ,0),
,0),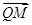 =
=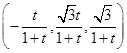 ,
,∴平面MBQ的法向量为m=(
 ,0,t).
,0,t).∵二面角M—BQ—C为30°,
cos 30°=
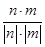 =
=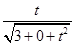 =
=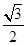 ,∴t=3.
,∴t=3.
练习册系列答案
相关题目
 中,
中, ⊥平面
⊥平面 ,
, ∥
∥ ,
, ,
, 分别为线段
分别为线段 的中点.
的中点.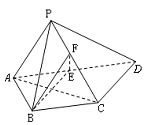
 ;
;  ⊥平面
⊥平面 .
. 中,
中, ,
, ,点
,点 为
为 的中点。
的中点。
 ∥平面
∥平面 ;
; 平面
平面 ;
;

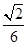 ,求线段AM的长.
,求线段AM的长.
 底面是菱形,
底面是菱形, ,
, ,
, 分别是
分别是 的中点.
的中点.
 ⊥平面
⊥平面 ;
;  是
是 上的动点,
上的动点, 与平面
与平面 ,求二面角
,求二面角 的正切值.
的正切值.
 中,
中, 平面
平面 ,
, ,
, ,
, .以
.以 ,
, 为邻边作平行四边形
为邻边作平行四边形 ,连接
,连接 和
和 .
.
 ∥平面
∥平面 ;
; 与平面
与平面 所成角的正弦值;
所成角的正弦值; ,使平面
,使平面 垂直?若存在,求出
垂直?若存在,求出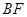 的长;若
的长;若 中,
中, 为
为 上一点,面
上一点,面 面
面 ,四边形
,四边形 为矩形
为矩形 ,
, ,
,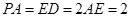 .
.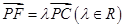 ,且
,且 ∥面
∥面 ,求
,求 的值;
的值; 面
面 ,并求点
,并求点 到面
到面 的距离.
的距离.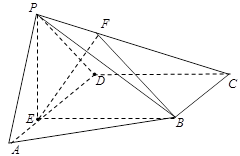
 是两条不同的直线,
是两条不同的直线,  是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( ) ,则
,则
 ,则
,则 ,则
,则
 ,则
,则