Question

【题目】设 ，向量 =（cosα，sinα）， ．
（1）证明：向量 与 垂直；
（2）当| |=| |时，求角α．

Answer 1

【答案】
（1）证明：由向量 =（cosα，sinα）， ，

得| |=1， =1，则 ，

所以向量 与 垂直

（2）解：将| |=| |两边平方，化简得3（| |2﹣| |2）+8 ，

由| |= =1，得 ，即 ．

所以 ，注意到 ，得

【解析】（1）计算| |， ，通过计算 ，证明向量 与 垂直；（2）将| |=| |两边平方，平方可得3（| |2﹣| |2）+8 ，从而得到以 ，然后求角α．
【考点精析】解答此题的关键在于理解数量积表示两个向量的夹角的相关知识，掌握设、都是非零向量，，，是与的夹角，则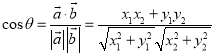，以及对数量积判断两个平面向量的垂直关系的理解，了解若平面的法向量为，平面的法向量为，要证，只需证，即证;即：两平面垂直两平面的法向量垂直．