题目内容
在平面直角坐标系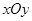 中,平面区域
中,平面区域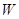 中的点的坐标
中的点的坐标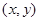 满足
满足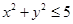 ,从区域
,从区域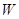 中随机取点
中随机取点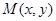 .
.
(Ⅰ)若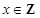 ,
,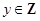 ,求点
,求点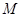 位于第四象限的概率;
位于第四象限的概率;
(Ⅱ)已知直线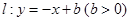 与圆
与圆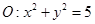 相交所截得的弦长为
相交所截得的弦长为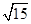 ,求
,求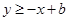 的概率.
的概率.
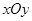 中,平面区域
中,平面区域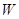 中的点的坐标
中的点的坐标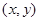 满足
满足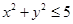 ,从区域
,从区域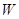 中随机取点
中随机取点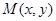 .
.(Ⅰ)若
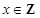 ,
,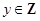 ,求点
,求点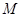 位于第四象限的概率;
位于第四象限的概率;(Ⅱ)已知直线
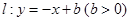 与圆
与圆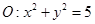 相交所截得的弦长为
相交所截得的弦长为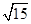 ,求
,求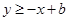 的概率.
的概率. (Ⅰ)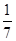 ;(Ⅱ)
;(Ⅱ)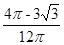 。
。
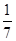 ;(Ⅱ)
;(Ⅱ)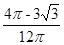 。
。试题分析:(Ⅰ)若
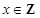 ,
,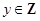 ,则点
,则点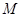 的个数共有
的个数共有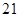 个,列举如下:
个,列举如下: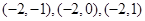 ;
;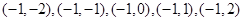 ;
;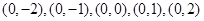 ;
;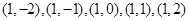 ;
;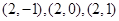 .
.当点
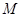 的坐标为
的坐标为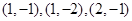 时,点
时,点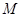 位于第四象限.
位于第四象限.故点
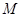 位于第四象限的概率为
位于第四象限的概率为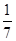 .
.(Ⅱ)由已知可知区域
 的面积是
的面积是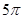 .
.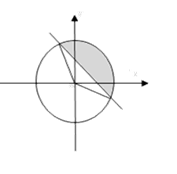
因为直线
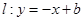 与圆
与圆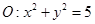 的弦长为
的弦长为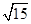 ,如图,可求得扇形的圆心角为
,如图,可求得扇形的圆心角为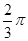 ,所以扇形的面积为
,所以扇形的面积为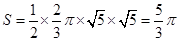 ,则满足
,则满足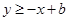 的点
的点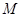 构成的区域的面积为
构成的区域的面积为
|
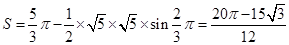 ,所以
,所以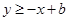 的概率为
的概率为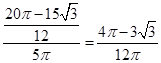 .考点:
.考点:点评:注意古典还行与几何概型的区别:。古典概型:试验中所有可能出现的基本事件只有有限个;几何概型:试验中所有可能出现的基本事件有无限多个。

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
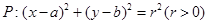 被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于
被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于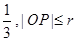 (其中
(其中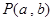 为圆心,O为坐标原点)。
为圆心,O为坐标原点)。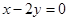 上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在
上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在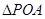 内”的概率的最大值
内”的概率的最大值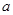 的正方体
的正方体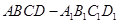 内任取一点
内任取一点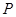 ,则点
,则点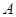 的距离小等于
的距离小等于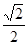


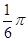
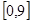 上随机取一实数
上随机取一实数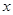 ,则该实数
,则该实数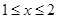 的概率为 .
的概率为 .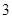 名男生
名男生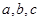 和
和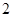 名女生
名女生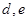 中任选
中任选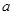 被选中的概率
被选中的概率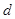 至少一人被选中的概率。
至少一人被选中的概率。



