题目内容
【题目】如图,边长为2的正方形ABCD中, 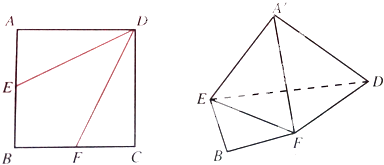
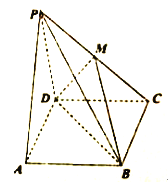
(1)点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.求证:A′D⊥EF
(2)当BE=BF= ![]() BC时,求三棱锥A′﹣EFD的体积.
BC时,求三棱锥A′﹣EFD的体积.
【答案】
(1)解:由正方形ABCD知,∠DCF=∠DAE=90°,
∴A'D⊥A'F,A'D⊥A'E,
∵A'E∩A'F=A',A'E、A'F平面A'EF.
∴A'D⊥平面A'EF.
又∵EF平面A'EF,
∴A'D⊥EF.
(2)解:由四边形ABCD为边长为2的正方形
故折叠后A′D=2,A′E=A′F= ![]() ,EF=
,EF= ![]()
则cos∠EA′F= 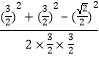 =
= ![]()
则sin∠EA′F= ![]()
故△EA′F的面积S△EA′F= ![]() A′EA′Fsin∠EA′F=
A′EA′Fsin∠EA′F= ![]()
由(1)中A′D⊥平面A′EF
可得三棱锥A'﹣EFD的体积V= ![]() ×
× ![]() ×2=
×2= ![]()
【解析】(1)由正方形ABCD知∠DCF=∠DAE=90°,得A'D⊥A'F且A'D⊥A'E,所以A'D⊥平面A'EF.结合EF平面A'EF,得A'D⊥EF;(2)由勾股定理的逆定理,得△A'EF是以EF为斜边的直角三角形,而A'D是三棱锥D﹣A'EF的高线,可以算出三棱锥D﹣A'EF的体积,即为三棱锥A'﹣DEF的体积.
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点,需要掌握垂直于同一个平面的两条直线平行才能正确解答此题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目