题目内容
已知命题p：?x∈R，使sinx=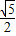
；命题q：?x∈R，都有x2+x+1＞0．下列结论中正确的（ ）A．命题“p∧q”是真命题
B．命题“p∧非q”是真命题
C．命题“非p∧q”是真命题
D．命题“非p∧q”是假命题
【答案】分析：首先判断命题p和q的真假，再利用真值表对照各选项选择．
命题p的真假有正弦函数的有界性判断，命题q的真假结合二次函数的图象只需看△．
解答：解：命题p：因为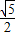
＞1，故不存在x∈R，使sinx=
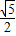，命题p为假；
命题q：△=1-4=-3＜0，故?x∈R，都有x2+x+1＞0为真．
A、命题“p∧q”是假命题，B、非q为假，故命题“p∧非q”是假命题，
C、非p为真，故命题“非p∧q”是真命题
故选C
点评：本题考查命题和复合命题真假的判断、正弦函数的有界性及二次函数恒成立等知识，属基本题型的考查．
命题p的真假有正弦函数的有界性判断，命题q的真假结合二次函数的图象只需看△．
解答：解：命题p：因为
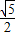＞1，故不存在x∈R，使sinx=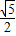，命题p为假；命题q：△=1-4=-3＜0，故?x∈R，都有x2+x+1＞0为真．
A、命题“p∧q”是假命题，B、非q为假，故命题“p∧非q”是假命题，
C、非p为真，故命题“非p∧q”是真命题
故选C
点评：本题考查命题和复合命题真假的判断、正弦函数的有界性及二次函数恒成立等知识，属基本题型的考查．
练习册系列答案
相关题目