题目内容
 某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(n≥10,n∈N*)为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.
某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(n≥10,n∈N*)为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.(1)记以Pn为圆心的圆与主干道Ox切于An点,证明:数列{
| 1 |
| xn |
(2)记⊙Pn的面积为Sn,根据以往施工经验可知,面积为S的圆型小道的施工工时为
| πS |
分析:(1)依题意可设⊙pn的半径rn=yn=xn2,由题意可得|pnpn+1|=rn+rn+1,代入点的坐标整理可得
-
=2,结合等差数列的通项公式可求
,进而可求xn,即可求解
(2)由sn=πrn2=πxn4=
,代入Tn=
+
+…+
=π[
+
+…+
],利用放缩法及裂项即可求解和,可求
| 1 |
| xn+1 |
| 1 |
| xn |
| 1 |
| xn |
(2)由sn=πrn2=πxn4=
| π |
| (2n-1)4 |
| πs1 |
| πs2 |
| πsn |
| 1 |
| 12 |
| 1 |
| 32 |
| 1 |
| (2n-1)2 |
解答:解:(1)依题意可设⊙pn的半径rn=yn=xn2
∵⊙pn与⊙pn+1相切
∴|pnpn+1|=rn+rn+1
∴
+
=yn+yn+1
两边平方整理可得,(xn-xn+1)2=4xn2xn+12
∵xn>xn+1>0
∴xn-xn+1=2xnxn+1
∴
-
=2
∴{
}是以1为首项,以2为公差的等差数列
∴
=1+2(n-1)=2n-1
∴xn=
即|OAn|=
(2)∵sn=πrn2=πxn4=
设前几个圆型小道的施工总时为Tn=
+
+…+
=π[
+
+…+
]
<π[1+
+
+…+
]
=π[1+
(1-
+
-
+…+
-
]
=π[1+
(1-
)]=
π<
<5
故5周内完成修建工作
∵⊙pn与⊙pn+1相切
∴|pnpn+1|=rn+rn+1
∴
| (xn-xn+1)2 |
| (yn-yn+1)2 |
两边平方整理可得,(xn-xn+1)2=4xn2xn+12
∵xn>xn+1>0
∴xn-xn+1=2xnxn+1
∴
| 1 |
| xn+1 |
| 1 |
| xn |
∴{
| 1 |
| xn |
∴
| 1 |
| xn |
∴xn=
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
(2)∵sn=πrn2=πxn4=
| π |
| (2n-1)4 |
设前几个圆型小道的施工总时为Tn=
| πs1 |
| πs2 |
| πsn |
=π[
| 1 |
| 12 |
| 1 |
| 32 |
| 1 |
| (2n-1)2 |
<π[1+
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| (2n-3)(2n-1) |
=π[1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-3 |
| 1 |
| 2n-1 |
=π[1+
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 3n-2 |
| 2n-1 |
| 3π |
| 2 |
故5周内完成修建工作
点评:本题主要考查了圆外切性质的应用,利用数列的递推公式构造等差数列求解通项公式,数列的裂项求和及放缩法在不等式中的应用

练习册系列答案
相关题目

 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线 的一段,在小道上依次以点
的一段,在小道上依次以点 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若 (单位:百米)且
(单位:百米)且 .
. 为圆心的圆与主干道
为圆心的圆与主干道 点,证明:数列
点,证明:数列 是等差数列,并求
是等差数列,并求 关于
关于 的表达式;
的表达式; 的面积为
的面积为 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为 的圆型小道的施工工时为
的圆型小道的施工工时为 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前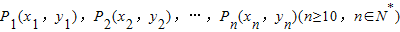 为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.
为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn. 是等差数列,并求|OAn|关于n的表达式;
是等差数列,并求|OAn|关于n的表达式; (单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.
(单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.
 为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.
为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn. 是等差数列,并求|OAn|关于n的表达式;
是等差数列,并求|OAn|关于n的表达式; (单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.
(单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.
 为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.
为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn. 是等差数列,并求|OAn|关于n的表达式;
是等差数列,并求|OAn|关于n的表达式; (单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.
(单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.