题目内容

实系数方程x2+ax+2b=0的两根为x1、x2，且0＜x1＜1＜x2＜2,则的取值范围是(    )

A.（，1）                                    B.（，1）

C.（-，）                                 D.（-，）

A

解析：设f(x)=x2+ax+2b，方程x2+ax+2b=0两根满足0＜x1＜1＜x2＜2的充要条件是:

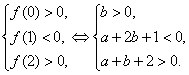
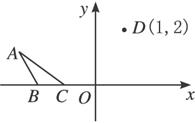
记A(-3,1),B(-2,0),C（-1，0）,则动点(a,b)表示△ABC内部的点集；而表示点（a,b）与D（1，2）连线的斜率kAD=,kCD=1，

∴＜＜1.

练习册系列答案
相关题目
已知实系数方程x2+ax+2b=0的一个根大于0且小于1，另一根大于1且小于2，则
b-2
a-1
的取值范围是（　　）
A、（
1
4
，1）
B、（
1
2
，1）
C、（-
1
2
，
1
4
）
D、（0，
1
3
）
实系数方程x2+ax+2b=0的一个根大于0且小于1，另一个根大于1且小于2，则
b-2a-1
的取值范围是
 
．
14、若关于x的实系数方程x2+ax+b=0有两个根，一个根在区间（0，1）内，另一根在区间（1，3）内，记点（a，b）对应的区域为S．设z=2a-b，则z的取值范围
（-11，-2）
．
关于x的实系数方程x2+ax+2b=0的一根在（0，1）内，另一根在（1，2）内，则点（a，b）所在区域的面积为
1
2
1
2
．
（2013•虹口区一模）若2-i是关于x的实系数方程x2+ax+b=0的一根，则该方程两根的模的和为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网