题目内容
关于x的实系数方程x2+ax+2b=0的一根在（0，1）内，另一根在（1，2）内，则点（a，b）所在区域的面积为
．
| 1 |
| 2 |
| 1 |
| 2 |
分析：设f（x）=x2+ax+2b，则有
成立，画出满足约束条件的可行域，即可求出面积．
|
解答：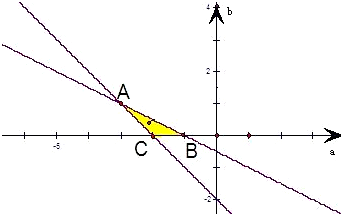
解：设f（x）=x2+ax+2b，由题意得：
，即
，
在坐标系aOb中画出上述不等式组表示的平面区域，
由题意，约束条件表示的平面区域为阴影部分（不包括边界）．其中A（-3，1），B（-1，0），C（-2，0）
根据平面区域，易求得点（a，b）所在区域的面积为
×BC×h=
×1×1=
．
故答案为：
．
解：设f（x）=x2+ax+2b，由题意得：
|
|
在坐标系aOb中画出上述不等式组表示的平面区域，
由题意，约束条件表示的平面区域为阴影部分（不包括边界）．其中A（-3，1），B（-1，0），C（-2，0）
根据平面区域，易求得点（a，b）所在区域的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题主要考查了简单的线性规划，函数零点的判定定理，以及利用几何意义求面积，属于基础题．
练习册系列答案
相关题目