题目内容
实系数方程x2+ax+2b=0的一个根大于0且小于1,另一个根大于1且小于2,则| b-2 | a-1 |
分析:先设f(x)=x2+ax+2b,数形结合容易得到使实系数方程,根据根的分布得出关于a,b的约束条件,设z=
表示的是区域内的点与原点(1,2)的斜率.故 z的最值问题即为直线的斜率的最大值与最小值.
| b-2 |
| a-1 |
解答: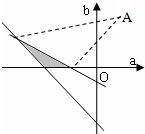 解:f(x)=x2+ax+2b,数形结合容易得到使实系数方程
解:f(x)=x2+ax+2b,数形结合容易得到使实系数方程
x2+ax+2b=0的两根分别在(0,1)和(1,2)内当且仅当:
?
点P(a,b)的可行域如右,
记A(1,2),线段PA的斜率为kPA,
kPA=
∈(
,1).
故答案为:(
,1).
 解:f(x)=x2+ax+2b,数形结合容易得到使实系数方程
解:f(x)=x2+ax+2b,数形结合容易得到使实系数方程x2+ax+2b=0的两根分别在(0,1)和(1,2)内当且仅当:
|
|
记A(1,2),线段PA的斜率为kPA,
kPA=
| b-2 |
| a-1 |
| 1 |
| 4 |
故答案为:(
| 1 |
| 4 |
点评:本题只是直接考查线性规划问题,巧妙识别目标函数的几何意义是我们研究规划问题的基础,纵观目标函数包括线性的与非线性,非线性问题的介入是线性规划问题的拓展与延伸,使得规划问题得以深化.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知实系数方程x2+ax+2b=0的一个根大于0且小于1,另一根大于1且小于2,则
的取值范围是( )
| b-2 |
| a-1 |
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(0,
|