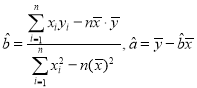题目内容
【题目】已知函数![]() .
.
(1)证明:当![]() 时,
时,![]() 有且仅有一个零点.
有且仅有一个零点.
(2)当![]() ,函数
,函数![]() 的最小值为
的最小值为![]() ,求函数
,求函数![]() 的值域.
的值域.
【答案】(1)详见解析(2)![]()
【解析】
(1)利用导数求得函数![]() 的单调区间和最小值,结合零点存在性定理,证得结论成立.(2)先求得
的单调区间和最小值,结合零点存在性定理,证得结论成立.(2)先求得![]() 得到解析式和导函数.根据(1)的结论,求得导函数的零点
得到解析式和导函数.根据(1)的结论,求得导函数的零点![]() ,根据
,根据![]() 将
将![]() 转化为
转化为![]() 的形式,进而求得
的形式,进而求得![]() 最小值的表达式,利用构造函数法和导数作为工具,求得
最小值的表达式,利用构造函数法和导数作为工具,求得![]() 最小值的取值范围,进而求得
最小值的取值范围,进而求得![]() 的取值范围.
的取值范围.
(1)证明:因为![]() ,所以
,所以![]() .
.
令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() ,则
,则![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故
上单调递增,故![]() ,因为
,因为![]() ,所以
,所以![]() ,所以当
,所以当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上没有零点,因为
上没有零点,因为![]() ,所以当
,所以当![]() 时,
时,![]() ,因为
,因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 有且仅有一个零点综上,当
有且仅有一个零点综上,当![]() 时,
时,![]() 有且仅有一个零点.
有且仅有一个零点.
(2)解:因为![]() ,所以
,所以![]() .
.
由(1)知当![]() 时,
时,![]() 有且仅有一个零点,因为
有且仅有一个零点,因为![]() ,
,![]() ,所以存在唯一
,所以存在唯一![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以
上单调递增,所以
![]() ,又
,又![]() ,即
,即![]() ,代入上式得,
,代入上式得,
![]() ,
,![]() ,设函数
,设函数![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递减,故
上单调递减,故![]() ,因为函数
,因为函数![]() 在
在![]() 上单调递减,故对任意
上单调递减,故对任意![]() ,存在唯一的
,存在唯一的![]() ,
,![]() ,使得
,使得![]() ,所以
,所以![]() 的值域是
的值域是![]() ,综上,当
,综上,当![]() 时,函数
时,函数![]() 的最小值
的最小值![]() 的值域为
的值域为![]()

练习册系列答案
相关题目
【题目】假设某种设备使用的年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有以下统计资料:
(万元)有以下统计资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系.试求:
呈线性相关关系.试求:
(1)求![]() ;
;
(2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算![]() 的值时,可根据以下公式:
的值时,可根据以下公式: