题目内容
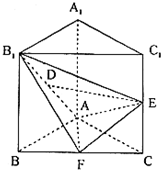 (2005•东城区一模)已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=a,D、E、F分别为B1A、C1C、BC的中点.
(2005•东城区一模)已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=a,D、E、F分别为B1A、C1C、BC的中点.(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求二面角B1-AF-B的大小(用反三角函数表示);
(Ⅲ)求三棱锥F-B1AE的体积.
分析:(I)连接A1B、A1E,并延长A1E交AC的延长线于点P,连接BP.通过证得DE∥BP来证明DE∥平面ABC;
(Ⅱ)∠B1FB应为二面角B1-AF-B的平面角.在Rt△B1BF中求解.
(Ⅲ)利用体积转化法求得VF-B1AE=VB1-AFE=
S△AEF×B1F=
×
×AF×EF×B1F=
a3
(Ⅱ)∠B1FB应为二面角B1-AF-B的平面角.在Rt△B1BF中求解.
(Ⅲ)利用体积转化法求得VF-B1AE=VB1-AFE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 8 |
解答:解:(I)连接A1B、A1E,并延长A1E交AC的延长线于点P,连接BP.
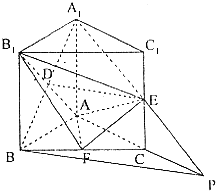
由E为C1C的中点,A1C1∥CP可证A1E=EP
∵D、E是A1B、A1P的中点,∴DE∥BP
又∵BP?平面ABC,DE?平面ABC,
∴DE∥平面ABC (5分)
(II)∵△ABC为等腰直角三角形,∠BAC=90°
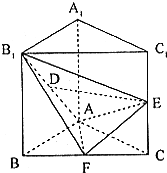
F为BC的中点,∴BC⊥AF
又∵B1B⊥平面ABC,由三垂线定理可证B1F⊥AF.
∴∠B1FB为二面角B1-AF-B的平面角.
在Rt△B1BF中,∠B1BF=90°,由B1B=a,BF=
a,
可求tan∠B1FB=
=
∴∠B1FB=arctan
∴二面角B1-AF-B的大小为arctan
(10分)
(III)又∵B1F2=
a2,EF2=
a2,B1E2=
a2
∴B1F2+EF2=B1E2
∴B1F=FE,∵B1F⊥AF,FE∩AF=F
∴B1F⊥平面AEF.
∵C1C⊥平面ABC,AF⊥FC,由三垂线定理可证EF⊥AF
∴VF-B1AE=VB1-AFE=
S△AEF×B1F=
×
×AF×EF×B1F=
a3

由E为C1C的中点,A1C1∥CP可证A1E=EP
∵D、E是A1B、A1P的中点,∴DE∥BP
又∵BP?平面ABC,DE?平面ABC,
∴DE∥平面ABC (5分)
(II)∵△ABC为等腰直角三角形,∠BAC=90°

F为BC的中点,∴BC⊥AF
又∵B1B⊥平面ABC,由三垂线定理可证B1F⊥AF.
∴∠B1FB为二面角B1-AF-B的平面角.
在Rt△B1BF中,∠B1BF=90°,由B1B=a,BF=
| ||
| 2 |
可求tan∠B1FB=
| B1B |
| BF |
| 2 |
∴∠B1FB=arctan
| 2 |
∴二面角B1-AF-B的大小为arctan
| 2 |
(III)又∵B1F2=
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
∴B1F2+EF2=B1E2
∴B1F=FE,∵B1F⊥AF,FE∩AF=F
∴B1F⊥平面AEF.
∵C1C⊥平面ABC,AF⊥FC,由三垂线定理可证EF⊥AF
∴VF-B1AE=VB1-AFE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 8 |
点评:本题考查空间直线、平面位置关系的判断,二面角大小求解,体积的计算考查空间想象能力、推理论证、计算、转化能力.

练习册系列答案
相关题目