题目内容
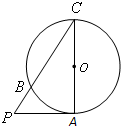 (《几何证明选讲》选做题)如图:已知PA是圆O的切线,切点为A,
(《几何证明选讲》选做题)如图:已知PA是圆O的切线,切点为A,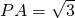 .AC是圆O的直径,PC与圆O交于B点,BC=2,则圆O的半径R=________.
.AC是圆O的直径,PC与圆O交于B点,BC=2,则圆O的半径R=________.
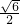
分析:先根据切割线定理求出PB,求出连接AB,根据弦切角定理及三角形相似的判定,我们易得△PBA~△PAC,再由相似三角形的性质,我们可以建立未知量与已知量之间的关系式,解方程即可求解.
解答:依题意,PA2=PB•PC?PB=1.
我们知道△PBA~△PAC,
由相似三角形的对应边成比例性质我们有
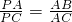 =
=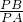 ,
,即
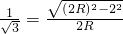 ?R=
?R= .
.故答案为:
 .
.点评:在平面几何中,我们要求线段的长度,关键是寻找未知量与已知量之间的关系,寻找相似三角形和全等三角形是常用的方法,根据相似三角形的性质,很容易得到已知量与未知量之间的关系,解方程即可求解

练习册系列答案
相关题目
 (几何证明选讲选选做题)如图,AC是⊙O的直径,B是⊙O上一点,∠ABC的平分线与⊙O相交于.D已知BC=1,AB=
(几何证明选讲选选做题)如图,AC是⊙O的直径,B是⊙O上一点,∠ABC的平分线与⊙O相交于.D已知BC=1,AB= (2012•江苏)A.[选修4-1:几何证明选讲]
(2012•江苏)A.[选修4-1:几何证明选讲]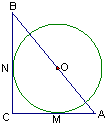 (2009•越秀区模拟)(《几何证明选讲》选做题)如图,在Rt△ABC中,∠C=90°,⊙O分别切AC、BC于M、N,圆心O在AB上,⊙O的半径为4,OA=5,则OB的长为
(2009•越秀区模拟)(《几何证明选讲》选做题)如图,在Rt△ABC中,∠C=90°,⊙O分别切AC、BC于M、N,圆心O在AB上,⊙O的半径为4,OA=5,则OB的长为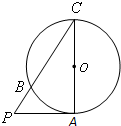 (2010•深圳模拟)(《几何证明选讲》选做题)如图:已知PA是圆O的切线,切点为A,
(2010•深圳模拟)(《几何证明选讲》选做题)如图:已知PA是圆O的切线,切点为A,