题目内容
 (2012•江苏)A.[选修4-1:几何证明选讲]
(2012•江苏)A.[选修4-1:几何证明选讲]如图,AB是圆O的直径,D,E为圆上位于AB异侧的两点,连接BD并延长至点C,使BD=DC,连接AC,AE,DE.
求证:∠E=∠C.
B.[选修4-2:矩阵与变换]
已知矩阵A的逆矩阵A-1=
|
C.[选修4-4:坐标系与参数方程]
在极坐标中,已知圆C经过点P(
| 2 |
| π |
| 4 |
| π |
| 3 |
| ||
| 2 |
D.[选修4-5:不等式选讲]
已知实数x,y满足:|x+y|<
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 18 |
分析:A.要证∠E=∠C,就得找一个中间量代换,一方面考虑到∠B,∠E是同弧所对圆周角,相等;另一方面根据线段中垂线上的点到线段两端的距离相等和等腰三角形等边对等角的性质得到.从而得证.
B.由矩阵A的逆矩阵,根据定义可求出矩阵A,从而求出矩阵A的特征值.
C.根据圆心为直线ρsin(θ-
)=-
与极轴的交点求出的圆心坐标;根据圆经过点P(
,
),求出圆的半径,从而得到圆的极坐标方程.
D.根据绝对值不等式的性质求证.
B.由矩阵A的逆矩阵,根据定义可求出矩阵A,从而求出矩阵A的特征值.
C.根据圆心为直线ρsin(θ-
| π |
| 3 |
| ||
| 2 |
| 2 |
| π |
| 4 |
D.根据绝对值不等式的性质求证.
解答: A.证明:连接 AD.
A.证明:连接 AD.
∵AB是圆O的直径,∴∠ADB=90°(直径所对的圆周角是直角).
∴AD⊥BD(垂直的定义).
又∵BD=DC,∴AD是线段BC 的中垂线(线段的中垂线定义).
∴AB=AC(线段中垂线上的点到线段两端的距离相等).
∴∠B=∠C(等腰三角形等边对等角的性质).
又∵D,E 为圆上位于AB异侧的两点,
∴∠B=∠E(同弧所对圆周角相等).
∴∠E=∠C(等量代换).
B、解:∵矩阵A的逆矩阵A-1=
,∴A=(A-1)-1=
]
∴f(λ)=
=λ2-3λ-4=0
∴λ1=-1,λ2=4
C、解:∵圆心为直线ρsin(θ-
)=-
与极轴的交点,
∴在ρsin(θ-
)=-中令θ=0,得ρ=1.∴圆C的圆心坐标为(1,0).
∵圆C 经过点P(
,
),∴圆C的半径为PC=1.
∴圆 的极坐标方程为ρ=2cosθ.
D、证明:∵3|y|=|3y|=|2(x+y)-(2x-y)|≤2|x+y|+2|2x-y|,:|x+y|<
,|2x-y|<
,
∴3|y|<
+
=
,
∴|y|<
 A.证明:连接 AD.
A.证明:连接 AD.∵AB是圆O的直径,∴∠ADB=90°(直径所对的圆周角是直角).
∴AD⊥BD(垂直的定义).
又∵BD=DC,∴AD是线段BC 的中垂线(线段的中垂线定义).
∴AB=AC(线段中垂线上的点到线段两端的距离相等).
∴∠B=∠C(等腰三角形等边对等角的性质).
又∵D,E 为圆上位于AB异侧的两点,
∴∠B=∠E(同弧所对圆周角相等).
∴∠E=∠C(等量代换).
B、解:∵矩阵A的逆矩阵A-1=
|
|
∴f(λ)=
|
∴λ1=-1,λ2=4
C、解:∵圆心为直线ρsin(θ-
| π |
| 3 |
| ||
| 2 |
∴在ρsin(θ-
| π |
| 3 |
∵圆C 经过点P(
| 2 |
| π |
| 4 |
∴圆 的极坐标方程为ρ=2cosθ.
D、证明:∵3|y|=|3y|=|2(x+y)-(2x-y)|≤2|x+y|+2|2x-y|,:|x+y|<
| 1 |
| 3 |
| 1 |
| 6 |
∴3|y|<
| 2 |
| 3 |
| 1 |
| 6 |
| 5 |
| 6 |
∴|y|<
| 5 |
| 18 |
点评:本题是选作题,综合考查选修知识,考查几何证明选讲、矩阵与变换、坐标系与参数方程、不等式证明,综合性强

练习册系列答案
相关题目
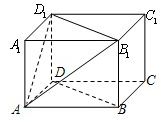 (2012•江苏)如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为
(2012•江苏)如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为