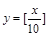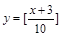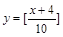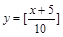题目内容
对于定义域为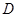 的函数
的函数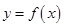 和常数
和常数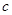 ,若对任意正实数
,若对任意正实数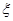 ,
,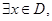 使得
使得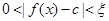 恒成立,则称函数
恒成立,则称函数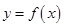 为“敛
为“敛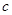 函数”.现给出如下函数:
函数”.现给出如下函数:
①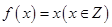 ; ②
; ②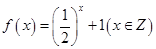 ;
;
③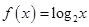 ; ④
; ④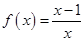 .
.
其中为“敛1函数”的有
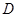 的函数
的函数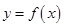 和常数
和常数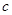 ,若对任意正实数
,若对任意正实数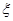 ,
,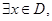 使得
使得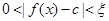 恒成立,则称函数
恒成立,则称函数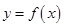 为“敛
为“敛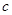 函数”.现给出如下函数:
函数”.现给出如下函数:①
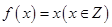 ; ②
; ②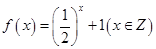 ;
;③
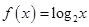 ; ④
; ④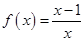 .
. 其中为“敛1函数”的有
| A.①② | B.③④ | C.②③④ | D.①②③ |
C
试题分析:根据题意,对于定义域为
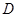 的函数
的函数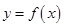 和常数
和常数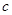 ,若对任意正实数
,若对任意正实数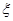 ,
,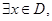 使得
使得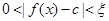 恒成立,则称函数
恒成立,则称函数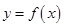 为“敛
为“敛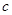 函数”.那么对于
函数”.那么对于①
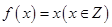 ;由于函数递增,那么不会存在一个正数
;由于函数递增,那么不会存在一个正数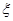 ,满足不等式。
,满足不等式。②
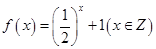 ;当x>0,c=2,那么存在x,满足题意,成立。
;当x>0,c=2,那么存在x,满足题意,成立。③
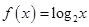 ;对于1<x<2,令c=1,,时符号题意。
;对于1<x<2,令c=1,,时符号题意。④
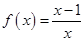 .=1-
.=1- ,x>1,c=3,则可知满足题意。故选C.
,x>1,c=3,则可知满足题意。故选C. 函数
函数点评:该试题有创新性,理解概念和运用概念,是解决试题的关键。

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 表示学生注意力随时间
表示学生注意力随时间 (分钟)的变化规律(
(分钟)的变化规律(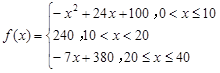
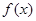 满足
满足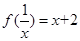 .
.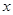 的方程
的方程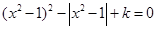 ,给出下列四个命题:
,给出下列四个命题: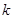 ,使得方程恰有2个不同实根; ②存在实数
,使得方程恰有2个不同实根; ②存在实数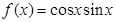 ,给出下列四个说法:
,给出下列四个说法: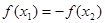 ,则
,则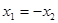 ,②点
,②点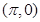 是
是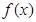 的一个对称中心,
的一个对称中心,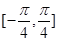 上是增函数,④
上是增函数,④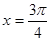 对称.
对称.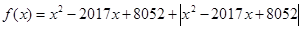 ,则
,则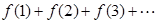
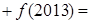 _ _.
_ _.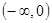 上是增函数的是( )
上是增函数的是( )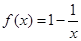
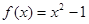
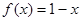
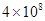 米)
米)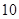 人推选一名代表,当各班人数除以
人推选一名代表,当各班人数除以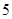 时再增选一名代表。那么,各班可推选代表人数
时再增选一名代表。那么,各班可推选代表人数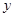 与该班人数
与该班人数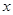 之间的函数关系用取整函数
之间的函数关系用取整函数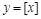 (
(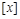 表示不大于
表示不大于