题目内容
19．同样大小的正方体木块堆放在房间的一个角落里，如图所示，问这些木块中看不见的木块有多少个？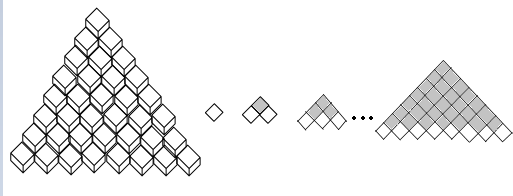
分析 根据已知归纳可得堆放n层共有：1+（1+2）+（1+2+3）+…+（1+2+3+…+n）=$\frac{n（n+1）（n+2）}{6}$个正方体木块，进而得到答案．
解答 解：由已知中正方体木块堆放方式可得：
堆放1层共有：1个正方体木块；
堆放2层共有：1+（1+2）个正方体木块；
堆放3层共有：1+（1+2）+（1+2+3）个正方体木块；
…
归纳可得：堆放n层共有：1+（1+2）+（1+2+3）+…+（1+2+3+…+n）=$\frac{n（n+1）（n+2）}{6}$个正方体木块；
由图可得：木块共堆放8层，故有$\frac{8×9×10}{6}$=120块．
点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
阅读快车系列答案
相关题目
14．抛物线y=$\frac{1}{4}$x2的焦点关于直线x-y-1=0的对称点的坐标是 （ ）
| A． | （2，-1） | B． | （1，-1） | C． | （$\frac{1}{4}$，-$\frac{1}{4}$） | D． | （$\frac{1}{16}$，-$\frac{1}{16}$） |