题目内容
为了解某班关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
 .
.(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由.
(2)现记不关注NBA的6名男生中某两人为a,b,关注NBA的10名女生中某3人为c,d,e,从这5人中选取2人进行调查,求:至少有一人不关注NBA的被选取的概率。
下面的临界值表,供参考
| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| K | 2.706 | 3.841 | 60635 | 7.879 |
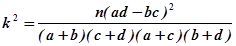 )其中n=a+b+c+d
)其中n=a+b+c+d
(1)有95%把握认为关注NBA与性别有关.(2)至少有一人不关注NBA的被选取的概率为P=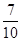 .
.
解析试题分析:(1)先根据已知条件把列联表补充完整,由公式计算 即可;(2)先列举从5人中选2人的基本事件,再列举至少有一人不关注NBA的事件,即可求得概率.
即可;(2)先列举从5人中选2人的基本事件,再列举至少有一人不关注NBA的事件,即可求得概率.
试题解析:(1)列联表补充如下:
(2分) 关注NBA 不关注NBA 合计 男生 22 6 28 女生 10 10 20 合计 32 16 48
由公式
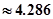 (5分)
(5分)
因为4.286>3.841.故有95%把握认为关注NBA与性别有关. (7分)
(2)从5人中选2人的基本事件有:ab,ac,ad.ae,bc,bd,be,cd,ce,de共10种,
其中至少有一人不关注NBA的有:ab,ac,ad,ae,bc,bd,be共7种,
故所求的概率为P=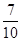 (13分)
(13分)
考点:独立性检验、古典概型.

 名校课堂系列答案
名校课堂系列答案在某次数学考试中,抽查了1000名学生的成绩,得到频率分布直方图如图所示,规定85分及其以上为优秀.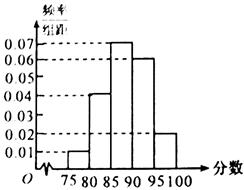
(1)下表是这次抽查成绩的频数分布表,试求正整数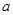 、
、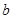 的值;
的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 50 | a | 350 | 300 | b |
(3)在根据(2)抽取的40名学生中,要随机选取2名学生参加座谈会,记其中成绩为优秀的人数为X,求X的分布列与数学期望(即均值).
从某校高二年级 名男生中随机抽取
名男生中随机抽取 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到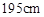 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组 ,第二组
,第二组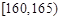 , ,第八组
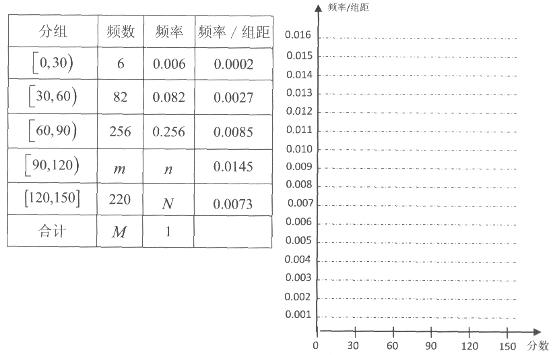
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
频率分布表如下:
| 分组 | 频数 | 频率 | 频率/组距 |
| | | | |
 |  | 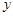 |  |
 |  |  |  |
| | | | |

(1)求频率分布表中所标字母的值,并补充完成频率分布直方图;
(2)若从身高属于第六组和第八组的所有男生中随机抽取
 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: 的事件的概率.
的事件的概率. 某工厂生产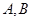 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
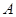 | 7 | 7 | 7.5 | 9 | 9.5 |
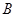 | 6 | 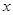 | 8.5 | 8.5 |  |
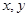 看不清,统计员只记得
看不清,统计员只记得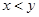 ,且
,且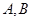 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(Ⅰ)求表格中
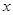 与
与 的值;
的值;(Ⅱ)若从被检测的5件
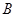 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率. 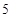 次预赛成绩记录如下:
次预赛成绩记录如下: 

 乙
乙 

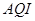 技术规定》(试行),
技术规定》(试行),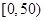 为优,
为优, 为良,
为良,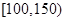 为轻度污染,
为轻度污染,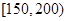 为中度污染,
为中度污染,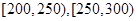 均为重度污染,
均为重度污染,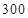 及以上为严重污染.某市2013年11月份
及以上为严重污染.某市2013年11月份 天的
天的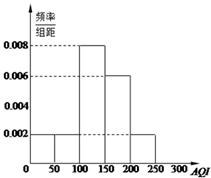
 天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天? 时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?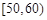 ,
,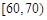 ,
,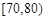 ,
,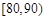 ,
,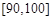 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
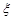 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在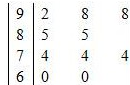
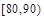 、
、 上的概率.
上的概率.