题目内容
已知定点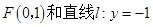 ,过点F且与直线
,过点F且与直线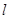 相切的动圆圆心为点M,记点M的轨迹为曲线E.
相切的动圆圆心为点M,记点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)若点A的坐标为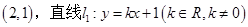 ,与曲线E相交于B,C两点,直线AB,AC分别交直线
,与曲线E相交于B,C两点,直线AB,AC分别交直线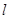 于点S,T.试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
于点S,T.试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
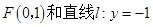 ,过点F且与直线
,过点F且与直线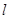 相切的动圆圆心为点M,记点M的轨迹为曲线E.
相切的动圆圆心为点M,记点M的轨迹为曲线E.(1)求曲线E的方程;
(2)若点A的坐标为
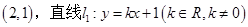 ,与曲线E相交于B,C两点,直线AB,AC分别交直线
,与曲线E相交于B,C两点,直线AB,AC分别交直线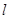 于点S,T.试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
于点S,T.试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.(1) .(2)以线段
.(2)以线段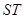 为直径的圆恒过两个定点
为直径的圆恒过两个定点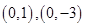 .
.
 .(2)以线段
.(2)以线段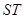 为直径的圆恒过两个定点
为直径的圆恒过两个定点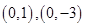 .
.试题分析:(1)根据抛物线的定义可知,点
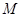 的轨迹是以点
的轨迹是以点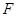 为焦点,
为焦点, 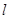 为准线的抛物线.
为准线的抛物线. 可得曲线
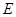 的方程为
的方程为 .
.(2)设点
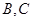 的坐标分别为
的坐标分别为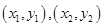 ,依题意得,
,依题意得,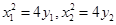 .
.由
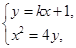 消去
消去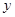 得
得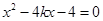 ,
,应用韦达定理
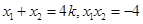 .
.直线
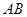 的斜率
的斜率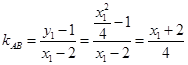 ,
,故直线
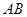 的方程为
的方程为 .
. 令
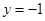 ,得
,得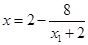 ,
,得到点
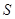 的坐标为
的坐标为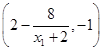 .点
.点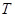 的坐标为
的坐标为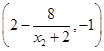 .
. 得到
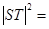
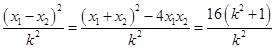 .
.设线段
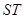 的中点坐标为
的中点坐标为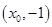 ,
,而
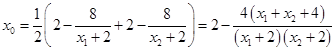
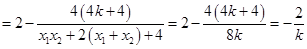 .
. 故以线段
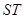 为直径的圆的方程为
为直径的圆的方程为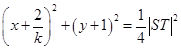
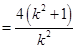 .
.令
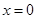 ,得
,得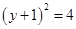 ,解得
,解得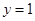 或
或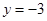 .
. 确定得到以线段
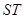 为直径的圆恒过两个定点
为直径的圆恒过两个定点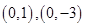 .
.(1)由题意, 点
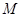 到点
到点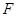 的距离等于它到直线
的距离等于它到直线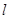 的距离,
的距离, 故点
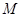 的轨迹是以点
的轨迹是以点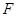 为焦点,
为焦点, 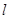 为准线的抛物线.
为准线的抛物线. ∴曲线
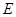 的方程为
的方程为 . 4分
. 4分(2)设点
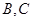 的坐标分别为
的坐标分别为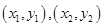 ,依题意得,
,依题意得,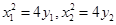 .
.由
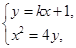 消去
消去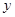 得
得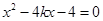 ,
,∴
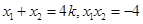 . 6分
. 6分 直线
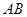 的斜率
的斜率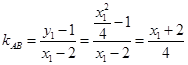 ,
,故直线
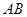 的方程为
的方程为 .
. 令
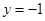 ,得
,得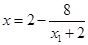 ,
,∴点
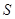 的坐标为
的坐标为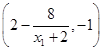 .
. 同理可得点
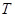 的坐标为
的坐标为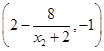 .
. ∴
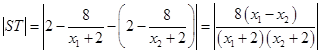
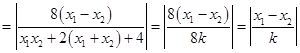 .
. ∴
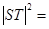
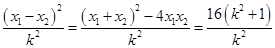 . 8分
. 8分设线段
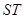 的中点坐标为
的中点坐标为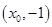 ,
,则
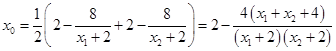
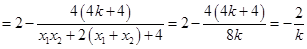 .
. ∴以线段
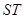 为直径的圆的方程为
为直径的圆的方程为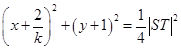
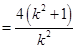 .
.展开得
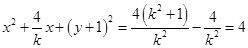 . 11分
. 11分 令
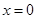 ,得
,得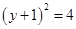 ,解得
,解得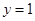 或
或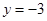 .
. ∴以线段
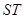 为直径的圆恒过两个定点
为直径的圆恒过两个定点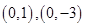 . 13分
. 13分
练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
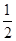 =0的距离等于( )
=0的距离等于( )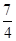 B.2 C.
B.2 C.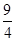 D.4
D.4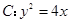 的焦点为
的焦点为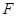 ,
,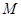 为抛物线
为抛物线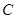 上一点,
上一点,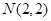 ,则
,则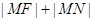 的取值范围是 .
的取值范围是 .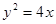 的顶点作射线
的顶点作射线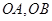 与抛物线交于
与抛物线交于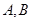 ,若
,若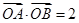 ,求证:直线
,求证:直线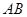 过定点.
过定点.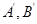 ,则
,则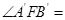 ( )
( )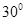 B.
B.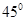 C.
C.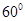 D.
D.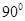
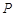 与定点
与定点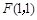 和直线
和直线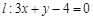 的距离相等,则动点
的距离相等,则动点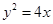 上一点
上一点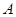 的横坐标为
的横坐标为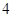 ,则点
,则点