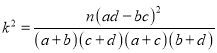题目内容
【题目】已知数集![]() ,其中
,其中![]() ,且
,且![]() ,若对
,若对![]() ,
,![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ,则称数集
,则称数集![]() 具有性质
具有性质![]() .
.
(1)分别判断数集![]() 与数集
与数集![]() 是否具有性质
是否具有性质![]() ,说明理由;
,说明理由;
(2)已知数集![]() 具有性质
具有性质![]() ,判断数列
,判断数列![]() ,
,![]() ,…,
,…,![]() 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
【答案】(1)数集![]() 不具有性质
不具有性质![]() ,数集
,数集![]() 具有性质
具有性质![]() ,理由见解析;(2)是等差数列,证明见解析
,理由见解析;(2)是等差数列,证明见解析
【解析】
(1)根据性质![]() 的定义逐个求差判断即可.
的定义逐个求差判断即可.
(2)根据性质![]() 的定义可先判断出
的定义可先判断出![]() ,再判断可得
,再判断可得![]() ,继而得到
,继而得到![]() 即可证明数列
即可证明数列![]() ,
,![]() ,…,
,…,![]() 为等差数列.
为等差数列.
解:(1)由于![]() 和
和![]() 都不属于集合
都不属于集合![]() ,
,
所以该集合不具有性质![]() ;
;
由于![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 都属于集合
都属于集合![]() ,
,
所以该数集具有性质![]() .
.
(2)∵![]() 具有性质
具有性质![]() ,所以
,所以![]() 与
与![]() 中至少有一个属于
中至少有一个属于![]() ,
,
由![]() ,有
,有![]() ,故
,故![]() ,∴
,∴![]() ,故
,故![]() .
.
∵![]() ,∴
,∴![]() ,故
,故![]() .
.
由![]() 具有性质
具有性质![]() 知,
知,![]() ,
,
又∵![]() ,
,
∴![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,
即![]() ①,
①,
由![]() 知,
知,![]() ,
,![]() ,…,
,…,![]() 均不属于
均不属于![]() ,
,
由![]() 具有性质
具有性质![]() ,
,![]() ,
,![]() ,…,
,…,![]() 均属于
均属于![]() ,
,
∴![]() ,而
,而![]() ,
,
∴![]() ,
,![]() ,
,![]() ,…,
,…,![]() 即
即![]() ②,
②,
由①②可知![]() ,
,
即![]() .
.
故![]() ,
,![]() ,…,
,…,![]() 构成等差数列.
构成等差数列.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
【题目】2014年非洲爆发了埃博拉病毒疫情,在疫情结束后,当地防疫部门做了一项回访调查,得到如下结果,
患病 | 不患病 | |
有良好卫生习惯 | 20 | 180 |
无良好卫生习惯 | 80 | 220 |
(1)结合上面列联表,是否有![]() 的把握认为是否患病与卫生习惯有关?
的把握认为是否患病与卫生习惯有关?
(2)现从有良好卫生习惯且不患病的180人中抽取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共5人,再从这5人中选两人给市民做健康专题报告,求
共5人,再从这5人中选两人给市民做健康专题报告,求![]() ,
,![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |