题目内容
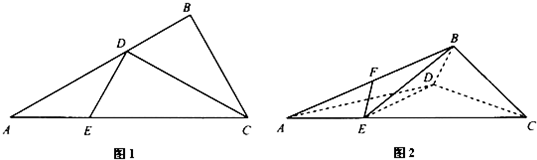
如图1,∠ACB=45°,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90°(如图2所示),
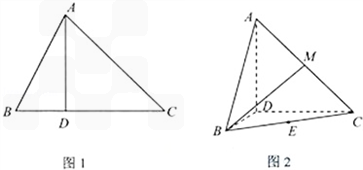
(1)当BD的长为多少时,三棱锥A-BCD的体积最大;
(2)当三棱锥A-BCD的体积最大时,设点E,M分别为棱BC,AC的中点,试在棱CD上确定一点N,使得EN⊥BM,并求EN与平面BMN所成角的大小。
(2)当三棱锥A-BCD的体积最大时,设点E,M分别为棱BC,AC的中点,试在棱CD上确定一点N,使得EN⊥BM,并求EN与平面BMN所成角的大小。
解:(1)设BD=x,则CD=3-x
∵∠ACB=45°,AD⊥BC,
∴AD=CD=3-x
∵折起前AD⊥BC,
∴折起后AD⊥BD,AD⊥CD,BD∩DC=D
∴AD⊥平面BCD
∴VA-BCD=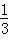 ×AD×S△BCD=
×AD×S△BCD=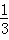 ×(3-x)×
×(3-x)×  ×x(3-x)=
×x(3-x)= 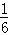 (x3-6x2+9x)
(x3-6x2+9x)
设f(x)=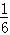 (x3-6x2+9x) x∈(0,3),
(x3-6x2+9x) x∈(0,3),
∵f′(x)= (x-1)(x-3),
(x-1)(x-3),
∴f(x)在(0,1)上为增函数,在(1,3)上为减函数
∴当x=1时,函数f(x)取最大值
∴当BD=1时,三棱锥A-BCD的体积最大。
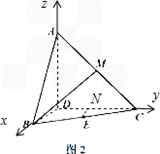
(2)以D为原点,建立如图直角坐标系D-xyz,
由(1)知,三棱锥A-BCD的体积最大时,BD=1,AD=CD=2
∴D(0,0,0),B(1,0,0),C(0,2,0),A(0,0,2),M(0,1,1),E( ,1,0),
,1,0),
且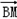 =(-1,1,1)设N(0,λ,0),
=(-1,1,1)设N(0,λ,0),
则 =(-
=(- ,λ-1,0)
,λ-1,0)
∵EN⊥BM,
∴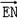 ·
·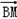 =0
=0
即(-1,1,1)(- ,λ-1,0)=
,λ-1,0)= +λ-1=0,
+λ-1=0,
∴λ= ,
,
∴N(0, ,0)
,0)
∴当DN= 时,EN⊥BM
时,EN⊥BM
设平面BMN的一个法向量为 =(x,y,z),
=(x,y,z),
由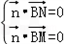 及
及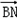 =(-1,
=(-1, ,0)得
,0)得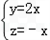 ,
,
取 =(1,2,-1)
=(1,2,-1)
设EN与平面BMN所成角为θ,
则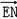 =(-
=(- ,
, ,0)
,0)
sinθ=|cos<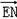 ,
, >|=|
>|=|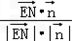 |=
|=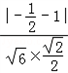 =
=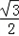
∴θ=60°
∴EN与平面BMN所成角的大小为60°
 。
。
∵∠ACB=45°,AD⊥BC,
∴AD=CD=3-x
∵折起前AD⊥BC,
∴折起后AD⊥BD,AD⊥CD,BD∩DC=D
∴AD⊥平面BCD
∴VA-BCD=
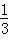 ×AD×S△BCD=
×AD×S△BCD=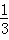 ×(3-x)×
×(3-x)×  ×x(3-x)=
×x(3-x)= 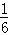 (x3-6x2+9x)
(x3-6x2+9x)设f(x)=
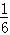 (x3-6x2+9x) x∈(0,3),
(x3-6x2+9x) x∈(0,3), ∵f′(x)=
 (x-1)(x-3),
(x-1)(x-3),∴f(x)在(0,1)上为增函数,在(1,3)上为减函数
∴当x=1时,函数f(x)取最大值
∴当BD=1时,三棱锥A-BCD的体积最大。
(2)以D为原点,建立如图直角坐标系D-xyz,
由(1)知,三棱锥A-BCD的体积最大时,BD=1,AD=CD=2
∴D(0,0,0),B(1,0,0),C(0,2,0),A(0,0,2),M(0,1,1),E(
 ,1,0),
,1,0),且
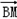 =(-1,1,1)设N(0,λ,0),
=(-1,1,1)设N(0,λ,0),则
 =(-
=(- ,λ-1,0)
,λ-1,0)∵EN⊥BM,
∴
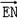 ·
·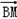 =0
=0即(-1,1,1)(-
 ,λ-1,0)=
,λ-1,0)= +λ-1=0,
+λ-1=0,∴λ=
 ,
,∴N(0,
 ,0)
,0)∴当DN=
 时,EN⊥BM
时,EN⊥BM设平面BMN的一个法向量为
 =(x,y,z),
=(x,y,z),由
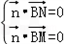 及
及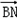 =(-1,
=(-1, ,0)得
,0)得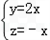 ,
,取
 =(1,2,-1)
=(1,2,-1)设EN与平面BMN所成角为θ,
则
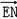 =(-
=(- ,
, ,0)
,0)sinθ=|cos<
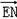 ,
, >|=|
>|=|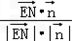 |=
|=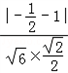 =
=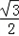
∴θ=60°
∴EN与平面BMN所成角的大小为60°
 。
。
练习册系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)