Question

【题目】已知双曲线的离心率为,过其右焦点作斜率为的直线，交双曲线的两条渐近线于两点（点在轴上方），则（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

由双曲线的离心率可得a＝b，求得双曲线的渐近线方程，设右焦点为（c，0），过其右焦点F作斜率为2的直线方程为y＝2（x﹣c），联立渐近线方程，求得B，C的坐标，再由向量共线定理，可得所求比值．

由双曲线的离心率为，可得ca，

即有a＝b，双曲线的渐近线方程为y＝±x，

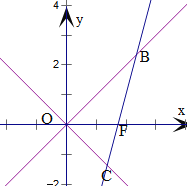
设右焦点为（c，0），过其右焦点F作斜率为2的直线方程为y＝2（x﹣c），

由y＝x和y＝2（x﹣c），可得B（2c，2c），

由y＝﹣x和y＝2（x﹣c）可得C（，），

设λ，即有0﹣2c＝λ（0），

解得λ＝3，即则3．

故选：B．