题目内容
设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)·g(x)+f(x)·g′(x)>0,且f(-3)·g(-3)=0,则不等式f(x)·g(x)<0的解集是( )
| A.(-3,0)∪(3,+∞) |
| B.(-3,0)∪ (0,3) |
| C.(-∞,-3)∪(3,+∞) |
| D.(-∞,-3)∪(0,3) |
D
解析试题分析:设F(x)="f" (x)g(x),当x<0时,∵F′(x)=f′(x)g(x)+f (x)g′(x)>0.∴F(x)在当x<0时为增函数.
∵F(-x)="f" (-x)g (-x)="-f" (x)•g (x)=-F(x).
故F(x)为(-∞,0)∪(0,+∞)上的奇函数.
∴F(x)在(0,∞)上亦为增函数.
已知f(-3)·g(-3)=0,必有F(-3)=F(3)=0.
构造如图的F(x)的图象,
可知F(x)<0的解集为x∈(-∞,-3)∪(0,3).
考点:本试题主要考查了复合函数的求导运算和函数的单调性与其导函数正负之间的关系.
点评:导数是一个新内容,也是高考的热点问题,要多注意复习.解决该试题的关键是先根据f’(x)g(x)+f(x)g’(x)>0可确定[f(x)g(x)]'>0,进而可得到f(x)g(x)在x<0时递增。

练习册系列答案
相关题目
函数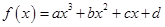 的图象(如图),则函数
的图象(如图),则函数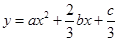 的单调递增区间是( )
的单调递增区间是( )
A.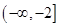 | B.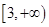 |
C.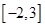 | D.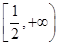 |
由直线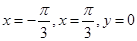 与曲线
与曲线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A.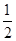 | B.1 | C.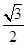 | D. |
函数 的导函数
的导函数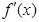 的图象大致是( )
的图象大致是( )
A. | B. |
C. | D. |
已知二次函数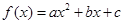 的导数为
的导数为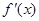 ,
,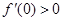 ,对于任意实数
,对于任意实数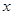 ,有
,有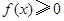 ,则
,则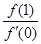 的最小值为
的最小值为
A.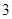 | B.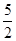 | C.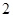 | D. |
已知定义在实数集 上的函数
上的函数 满足
满足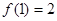 ,且
,且 的导函数
的导函数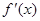 在
在 上恒有
上恒有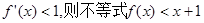 的解集为
的解集为
A.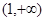 | B.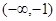 |
C.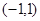 | D.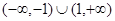 |
设函数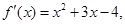 则
则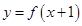 的单调减区间为( )
的单调减区间为( )
A.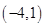 | B. |
C.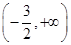 | D.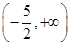 |



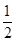

 上,
上, 为曲线在点P处的切线的倾斜角,则
为曲线在点P处的切线的倾斜角,则