题目内容
由直线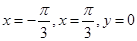 与曲线
与曲线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A.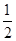 | B.1 | C.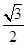 | D. |
B
解析试题分析:因为根据定积分的几何意义可知由直线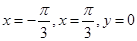 与曲线
与曲线 所围成的封闭图形的面积可以表示为
所围成的封闭图形的面积可以表示为 故选B
故选B
考点:本试题主要考查了利用定积分的基本定理,和定积分的几何意义来表示曲边梯形的面积的求解问题。
点评:解决该试题的关键是能利用定积分的几何意义准确表示出面积公式,注意先求解交点定积分上下限,并运用导数的公式得到原函数进而求解。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知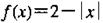 ,则
,则 = ( )
= ( )
| A.3 | B.4 | C.3.5 | D.4.5 |
设函数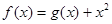 ,曲线
,曲线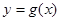 在点
在点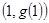 处的切线方程为
处的切线方程为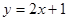 ,则曲线
,则曲线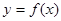 在点
在点 处的切线的斜率为( )
处的切线的斜率为( )
A.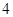 | B.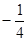 | C. | D.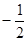 |
曲线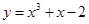 在点
在点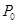 处的切线平行于直线
处的切线平行于直线 ,则点
,则点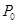 的坐标可为( )
的坐标可为( )
| A.(0,1) | B.(1,0) | C.(-1,0) | D.(1,4) |
已知某生产厂家的年利润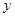 (单位:万元)与年产量
(单位:万元)与年产量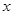 (单位:万件)的函数关系式为
(单位:万件)的函数关系式为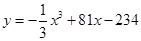 ,则使该生产厂家获得最大年利润的年产量为( ).
,则使该生产厂家获得最大年利润的年产量为( ).
| A.7万件 | B.9万件 |
| C.11 万件 | D.13万件 |
设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)·g(x)+f(x)·g′(x)>0,且f(-3)·g(-3)=0,则不等式f(x)·g(x)<0的解集是( )
| A.(-3,0)∪(3,+∞) |
| B.(-3,0)∪ (0,3) |
| C.(-∞,-3)∪(3,+∞) |
| D.(-∞,-3)∪(0,3) |
曲线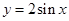 在点
在点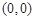 处的切线与直线
处的切线与直线 垂直,则实数
垂直,则实数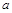 的值为( )
的值为( )
| A.2 | B.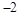 | C.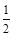 | D.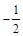 |
由曲线y=x2,y=x3围成的封闭图形面积为 ( )
A.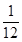 | B.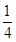 | C.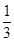 | D.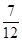 |
设函数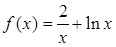 则 ? ?
则 ? ?
A.x=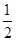 为f(x)的极大值点 为f(x)的极大值点 | B.x=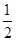 为f(x)的极小值点 为f(x)的极小值点 |
| C.x=2为 f(x)的极大值点 | D.x=2为 f(x)的极小值点 |