题目内容
函数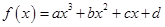 的图象(如图),则函数
的图象(如图),则函数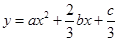 的单调递增区间是( )
的单调递增区间是( )
A.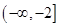 | B.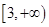 |
C.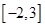 | D.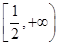 |
D
解析试题分析:因为函数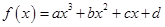 ,则f'(x)=3ax2+2bx+c,由图可知f'(-2)=0,f'(3)=0,∴12a-4b+c=0,27a+6b+c=0,∴b=-
,则f'(x)=3ax2+2bx+c,由图可知f'(-2)=0,f'(3)=0,∴12a-4b+c=0,27a+6b+c=0,∴b=- ,c=-18a,所以
,c=-18a,所以  ,则y’=a(2x-1)
,则y’=a(2x-1)
∴y=3ax2-3ax-18a,结合图像可知a>0,那么y'=a(2x-1),当x> 时,y'>0,∴y=x2-x-6的单调递增区间为:[
时,y'>0,∴y=x2-x-6的单调递增区间为:[ ,+∞),故选D.
,+∞),故选D.
考点:本试题主要考查了函数极值点和单调性与函数的导数之间的关系.属基础题.
点评:解决该试题的关键是通过图像确定出-2和3为函数的极值点,那么导数值为零,从而得到a,b,c,的关系式进而化简函数,求解导数得到单调区间。

练习册系列答案
相关题目
一物体在力 (
( 单位为
单位为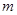 ,
, 单位为
单位为 )的作用下,沿着与力
)的作用下,沿着与力 相同的方向从
相同的方向从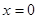 处运动到
处运动到 处,则力
处,则力 所作的功是:
所作的功是:
| A.40 | B.42 | C.48 | D.52 |
曲线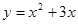 在点A(2,10)处的切线的斜率是
在点A(2,10)处的切线的斜率是
| A.4 | B.5 | C.6 | D.7 |
设函数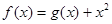 ,曲线
,曲线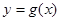 在点
在点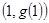 处的切线方程为
处的切线方程为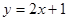 ,则曲线
,则曲线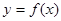 在点
在点 处的切线的斜率为( )
处的切线的斜率为( )
A.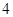 | B.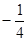 | C. | D.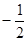 |
函数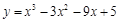 在区间
在区间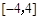 上的最大值为( ).
上的最大值为( ).
| A.10 | B.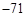 | C.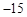 | D.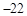 |
曲线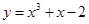 在点
在点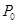 处的切线平行于直线
处的切线平行于直线 ,则点
,则点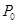 的坐标可为( )
的坐标可为( )
| A.(0,1) | B.(1,0) | C.(-1,0) | D.(1,4) |
已知某生产厂家的年利润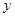 (单位:万元)与年产量
(单位:万元)与年产量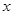 (单位:万件)的函数关系式为
(单位:万件)的函数关系式为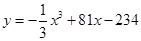 ,则使该生产厂家获得最大年利润的年产量为( ).
,则使该生产厂家获得最大年利润的年产量为( ).
| A.7万件 | B.9万件 |
| C.11 万件 | D.13万件 |
设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)·g(x)+f(x)·g′(x)>0,且f(-3)·g(-3)=0,则不等式f(x)·g(x)<0的解集是( )
| A.(-3,0)∪(3,+∞) |
| B.(-3,0)∪ (0,3) |
| C.(-∞,-3)∪(3,+∞) |
| D.(-∞,-3)∪(0,3) |
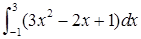 =( )
=( )
| A.24 | B.27 | C.28 | D.35 |