题目内容
(本小题共13分)
已知函数 .
.
(Ⅰ)若 在
在 处取得极值,求a的值;
处取得极值,求a的值;
(Ⅱ)求函数 在
在 上的最大值.
上的最大值.
【答案】
解:(Ⅰ)∵ ,
,
∴函数的定义域为 .
………………1分
.
………………1分
∴ …………3分
…………3分
∵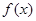 在
在 处取得极值,
处取得极值,
即 ,
,
∴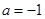 .
………………5分
.
………………5分
当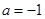 时,在
时,在 内
内 ,在
,在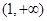 内
内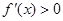 ,
,
∴ 是函数
是函数 的极小值点. ∴
的极小值点. ∴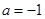 . ………………6分
. ………………6分
(Ⅱ)∵ ,∴
,∴ . ………………7分
. ………………7分

∵ x∈ , ∴
, ∴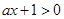 ,
,
∴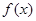 在
在 上单调递增;在
上单调递增;在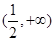 上单调递减,……………9分
上单调递减,……………9分
①当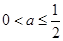 时,
时, 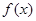 在
在 单调递增,
单调递增,
∴ ; ………………10分
; ………………10分
②当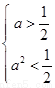 ,即
,即 时,
时,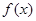 在
在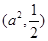 单调递增,在
单调递增,在 单调递减,
单调递减,
∴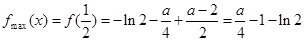 ; ………………11分
; ………………11分
③当 ,即
,即 时,
时,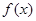 在
在 单调递减,
单调递减,
∴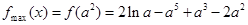 . ………………12分
. ………………12分
综上所述,当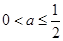 时,函数
时,函数 在
在 上的最大值是
上的最大值是 ;
;
当 时,函数
时,函数 在
在 上的最大值是
上的最大值是 ;
;
当 时,函数
时,函数 在
在 上的最大值是
上的最大值是 .………13分
.………13分
【解析】略

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 .
. 在
在 处取得极值,求a的值;
处取得极值,求a的值; 在
在 上的最大值.
上的最大值. ,设函数
,设函数 .
. 在
在 上的单调递增区间;
上的单调递增区间; 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, ,
, ,
, ,求边
,求边 ,求
,求
 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式; 的条件下,求
的条件下,求 的值.
的值.