题目内容
当x、y满足|x|+|y|≤1,则z=| x | y-3 |
分析:先根据约束条件画出可行域,设z=
,再利用z的几何意义求最值,其中式子z=
的形式可以联想成在区域内动点P与点(0,3)构成的直线的斜率,进而求解.
| x |
| y-3 |
| x |
| y-3 |
解答: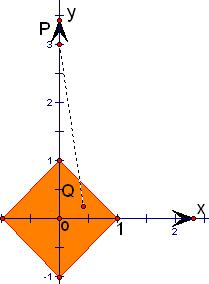 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,
设z=
,
将z的值转化成在区域内动点P与点(0,3)构成的直线的斜率,
当连线PQ经过点(1,0)时,z最小,
最小值为:-
.
当直线PQ经过点(1,0)关于原点的对称点时,z最大,
最大值为:
.
则z=
的取值范围是[-
,
]
故答案为[-
,
].
 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,设z=
| x |
| y-3 |
将z的值转化成在区域内动点P与点(0,3)构成的直线的斜率,
当连线PQ经过点(1,0)时,z最小,
最小值为:-
| 1 |
| 3 |
当直线PQ经过点(1,0)关于原点的对称点时,z最大,
最大值为:
| 1 |
| 3 |
则z=
| x |
| y-3 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为[-
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
相关题目
当x,y满足
时,则t=x+y的最大值是( )
|
| A、1 | B、2 | C、3 | D、5 |