题目内容
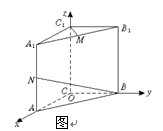
(14分)如图所示,直三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求 的长;
的长;
(2)求cos<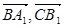 >的值;
>的值;
(3)求证:A1B⊥C1M.

【答案】
(1)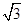 ;(2)
;(2)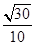 ;(3)见解析。
;(3)见解析。
【解析】
试题分析:如图,建立空间直角坐标系O—xyz.
(1)依题意得B(0,1,0)、N(1,0,1)
∴|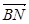 |=
|=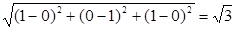 .
.
(2)依题意得A1(1,0,2)、B(0,1,0)、C(0,0,0)、B1(0,1,2)
∴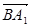 ={-1,-1,2},
={-1,-1,2},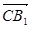 ={0,1,2,},
={0,1,2,},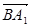 ·
·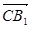 =3,|
=3,|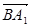 |=
|=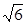 ,|
,|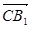 |=
|=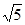
∴cos<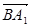 ,
,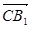 >=
>=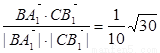 .
.
(3)证明:依题意,得C1(0,0,2)、M(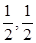 ,2),
,2),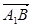 ={-1,1,2},
={-1,1,2},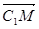 ={
={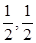 ,0}.∴
,0}.∴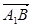 ·
·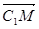 =-
=-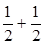 +0=0,∴
+0=0,∴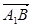 ⊥
⊥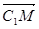 ,∴A1B⊥C1M.
,∴A1B⊥C1M.
考点:本题主要考查向量的坐标运算、数量积、模的概念及计算、夹角公式的应用,考查了考生的空间想象能力、逻辑推理能力。
点评:本题通过距离空间直角坐标系,将几何问题转化成空间向量,运用空间向量的基本知识,是“用数学”的好题.

练习册系列答案
相关题目
 如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点.
如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点. 如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记
如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记 如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
