题目内容
定义:F(x,y)=yx(x>0,y>0)(1)解关于x的不等式F(1,x2)+F(2,x)≤3x-1;
(2)记f(x)=3•F(1,x),设
 ,若不等式
,若不等式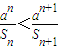 对n∈N*恒成立,求实数a的取值范围;
对n∈N*恒成立,求实数a的取值范围;(3)记g(x)=F(x,2),正项数列an满足:
 ,求数列an的通项公式,并求所有可能的乘积ai•aj(1≤i≤j≤n)的和.
,求数列an的通项公式,并求所有可能的乘积ai•aj(1≤i≤j≤n)的和.
【答案】分析:(1)有定义:F(x,y)=yx(x>0,y>0)先把关于x的不等式F(1,x2)+F(2,x)≤3x-1?x2+x2≤3x-1,然后求解一元二次不等式即可;
(2)有f(x)=3•F(1,x)得到f(x)的解析式,进而求得 ,然后利用不等式
,然后利用不等式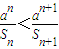 对n∈N*恒成立求解即可;
对n∈N*恒成立求解即可;
(3)有g(x)=F(x,2),且正项数列an满足: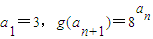 ,求出数列an的通项公式,即可.
,求出数列an的通项公式,即可.
解答:解:(1)有定义:F(x,y)=yx(x>0,y>0)得到:不等式F(1,x2)+F(2,x)≤3x-1?x2+x2≤3x-1⇒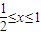 ;
;
(2)有f(x)=3•F(1,x)得到f(x)=3x∴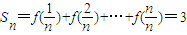
 =
=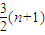 ,
,
∵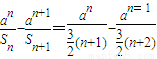 =
=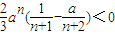 对n∈N*恒成立,
对n∈N*恒成立,
当a>0时,an>0,∴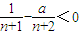 对n∈N*恒成立?
对n∈N*恒成立?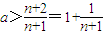 对n∈N*恒成立,易知
对n∈N*恒成立,易知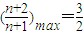 ,∴
,∴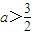
(3)∵g(x)=F(x,2),∴g(x)=2x,又正项数列an满足: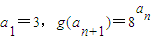 ,∴
,∴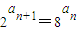 ⇒an+1=3an又a1=3
⇒an+1=3an又a1=3
∴an=3n⇒ai•aj=3i+j(o≤i≤j≤n),
将所得的积排成如下矩阵A=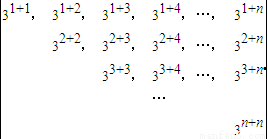 ,设该矩阵的各项和为S,由在矩阵的空格处填上相应的数可以得:
,设该矩阵的各项和为S,由在矩阵的空格处填上相应的数可以得:
矩阵B= ,
,
在矩阵B中第一行的所有数的和为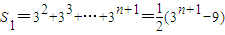 ;
;
在矩阵B中第二行的所有数的和为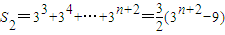 ;
;
…
点评:此题考查了一元二次不等式的求解,还考查了作差及不等式的恒成立及等比数列的求和.
(2)有f(x)=3•F(1,x)得到f(x)的解析式,进而求得
 ,然后利用不等式
,然后利用不等式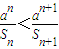 对n∈N*恒成立求解即可;
对n∈N*恒成立求解即可;(3)有g(x)=F(x,2),且正项数列an满足:
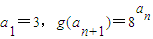 ,求出数列an的通项公式,即可.
,求出数列an的通项公式,即可.解答:解:(1)有定义:F(x,y)=yx(x>0,y>0)得到:不等式F(1,x2)+F(2,x)≤3x-1?x2+x2≤3x-1⇒
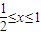 ;
;(2)有f(x)=3•F(1,x)得到f(x)=3x∴
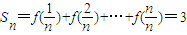
 =
=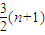 ,
,∵
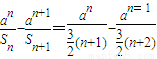 =
=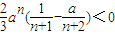 对n∈N*恒成立,
对n∈N*恒成立,当a>0时,an>0,∴
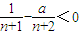 对n∈N*恒成立?
对n∈N*恒成立?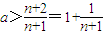 对n∈N*恒成立,易知
对n∈N*恒成立,易知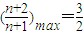 ,∴
,∴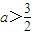
(3)∵g(x)=F(x,2),∴g(x)=2x,又正项数列an满足:
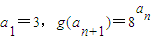 ,∴
,∴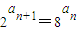 ⇒an+1=3an又a1=3
⇒an+1=3an又a1=3∴an=3n⇒ai•aj=3i+j(o≤i≤j≤n),
将所得的积排成如下矩阵A=
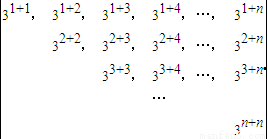 ,设该矩阵的各项和为S,由在矩阵的空格处填上相应的数可以得:
,设该矩阵的各项和为S,由在矩阵的空格处填上相应的数可以得:矩阵B=
 ,
,在矩阵B中第一行的所有数的和为
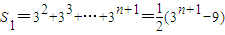 ;
;在矩阵B中第二行的所有数的和为
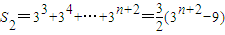 ;
;…
点评:此题考查了一元二次不等式的求解,还考查了作差及不等式的恒成立及等比数列的求和.

练习册系列答案
相关题目